Задача 5.
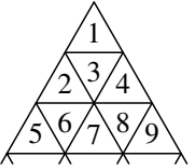
Каждая сторона равностороннего треугольника разбита на несколько равных частей по 1 см. Через точки деления проведены прямые, параллельные сторонам. Вася расставляет по строкам слева направо натуральные числа, начиная с 1 (см. рисунок). Его друг Петя выбрал горизонтальный отрезок, являющийся общей стороной двух маленьких треугольников. В одном из этих треугольников оказалось число 335. Какое число стоит в другом?
Ответ на Задачу 5.
Ответ: 373.
Решение:
Как нетрудно заметить, в $k$ −й строке расположены числа от ($k$ − 1)2 + 1 до $k^2$. Число 335 расположено в 19-й строке (в ней находятся числа от 325 до 361). При нечётном $k$ треугольники, примыкающие к нечётным числам, располагаются строчкой ниже. Под числом 325 находится 363. Сдвигаясь в обеих строках на 10 позиций вправо, мы получим, что под числом 335 находится число 373.

