Задача 1.
В одной из лекционных аудиторий Сибирского федерального университета 32 двухместные парты. Сейчас за ними сидят 64 первокурсника и слушают лекцию по математике. Известно, что 75% студентов мальчиков сидят рядом со студентами девочками, а 45% студентов девочек сидят рядом со студентами мальчиками. Сколько в аудитории студентов девочек?
Задача 2.
Четырнадцать одинаковых прямоугольников расположили так, как показано на рисунке. Какова площадь серой области в см2?
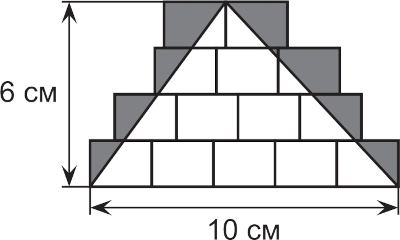
Задача 3.
Сколько существует треугольников, у которых вершины располагаются в отмеченных точках?
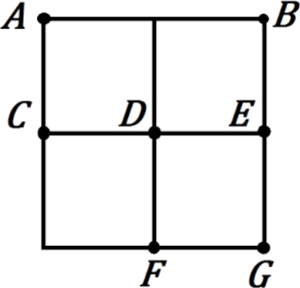
Задача 4.
У бельчонка есть чашечные весы и много орехов. На одну чашу весов он Положил орех массой 25 г, а затем последовательно на любую из чаш весов кладёт на чаши весов орехи массой 1 г, 2 г, 3 г и так далее (каждый следующий орех на один грамм тяжелее предыдущего). Какое наименьшее количество орехов ему потребуется, чтобы уравновесить чаши весов?
Задача 5.
Известно, что для различных натуральных чисел x, y и z справедливо равенство x + 2y + 3z = 990. Какое наибольшее значение может принимать наибольший общий делитель трёх чисел x, y и z?
Задача 6.
Семиклассник Саша разрезал пятиугольник $PQRST$ с периметром 50 см диагоналями $PR$ и $PS$ на три треугольника с периметрами 30 см каждый. Какова длина в см стороны пятиугольника $RS$?
Задача 7.
Бельчата Катя и Лена делят орехи. Если Катя возьмёт у Лены несколько орехов, то у неё станет орехов в 4 раза больше, чем у Лены. Если же Лена заберёт у Кати 90 орехов из её первоначального количества, то у Лены станет орехов в 5 раз больше, чем у Кати. Какое наименьшее количество орехов могло быть у Кати и Лены первоначально? В ответ запишите сумму орехов Кати и Лены.
Задача 8.
В финале чемпионата Сибирского федерального университета по туризму шесть спортсменов соревнуются по трём группам дисциплин. В каждой из дисциплин распределяются места с первого по шестое (делить одно и то же место нельзя) а финальный результат каждого спортсмена – произведение трёх занятых мест в каждой дисциплине. Оказалось, что утвержденные результаты таковы: Ваня – 5, Дима – 12, Женя – 24, Коля – 54, Миша – 64, Петя – 75. Определите, какие места заняли спортсмены в первой дисциплине, если известно, что Ваня показал в первой дисциплине самый слабый результат из всех трёх дисциплин.
Задача 9.
Известно, что любое число, стоящее в клетке на рисунке, равно сумме двух соседних с ним чисел. Какое число стоит в серой клетке?
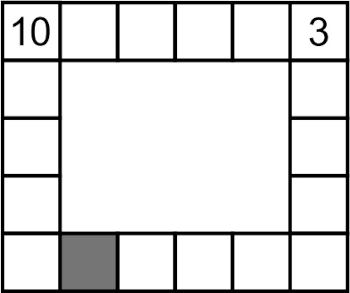
Задача 10.
Бельчонок расположил в ряд 2019 орехов и прикрепил к ним бумажки с номерами от 1 до 2019. Затем он поставил зелёную отметку на орехи, номера которых делятся на 3, потом поставил синюю отметку на орехи, номера которых делятся на 4, затем поставил красную отметку на орехи, номера которых делятся на 5, и, наконец, поставил жёлтую отметку на орехи, номера которых делятся на 7. Сколько орехов в ряду помечены ровно двумя отметками?

