Олимпиада «Бельчонок», 4 класс, 2021 год, 2 этап, 1 вариант
дата проведения: 6 марта 2021
Задача 5.
Два бельчонка, рыжий и серый, играют в такую игру. Они начертили на земле квадрат 7 × 7 клеток, в правую верхнюю клетку положили орех (на рисунке он обозначен буквой О). За один ход можно переложить орех на любое количество клеток или влево, или вниз. Кто первый положит орех в левую нижнюю клетку, тот выиграет. Первый ход делает рыжий бельчонок. Кто из бельчат всегда может выиграть?
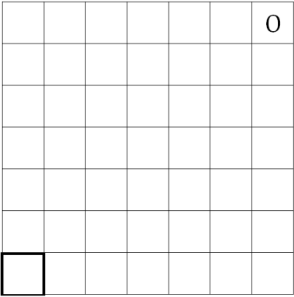
Ответ на Задачу 5.
Ответ: Серый бельчонок.
Решение:
После любого хода рыжего бельчонка серый бельчонок должен переложить орех в закрашенную клетку диагонали. С этих клеток невозможно за один ход попасть в правую верхнюю клетку, поэтому рыжий бельчонок не сможет выиграть, как бы он ни ходил.


