Задача 1.
15 бельчат собирали маслята и рыжики. 9 бельчат нашли маслята, из них 4 нашли и маслята, и рыжики. Сколько бельчат нашли рыжики?
Задача 2.
Коля, Алёна, и ещё 9 детей пошли в тир. Там было 8 мишеней, и каждый из 11 детей сделал по одному выстрелу в каждую мишень. В результате каждый из детей, кроме Алёны, попал одинаковое число раз, а Алёна попала 8 раз, и в каждую мишень попало 6 пуль. Сколько было попаданий у Коли?
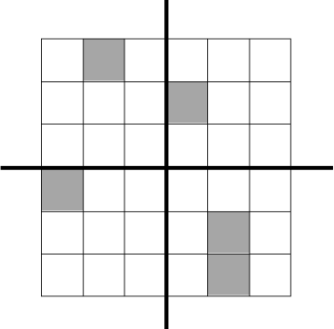
Задача 3.
В квадрате 6 × 6 некоторые клетки закрашены. Закрасьте ещё клетки, чтобы при сгибании квадрата по любой прямой из двух (см. рисунок) закрашенные клетки совмещались с белыми, а белые — с закрашенными. Сколько белых клеток останется?
Задача 4.
Во время перемены в классе остались четыре девочки: Аня, Вера, Катя и Лена.
- Аня сказала: «У меня тут нет подружек»,
- потом Вера заявила: «У меня тут ровно одна подружка»,
- затем добавила Катя: «У меня ровно две подружки»,
- последней сказала Лена: «А у меня три подружки!».
Оказалось, что девочки, имеющие чётное количество подружек, сказали правду, а имеющие нечётное — солгали. Кто с кем дружит?
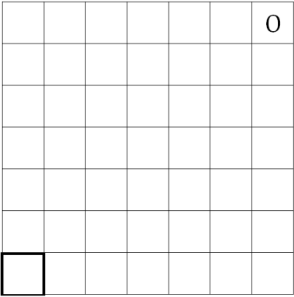
Задача 5.
Два бельчонка, рыжий и серый, играют в такую игру. Они начертили на земле квадрат 7 × 7 клеток, в правую верхнюю клетку положили орех (на рисунке он обозначен буквой О). За один ход можно переложить орех на любое количество клеток или влево, или вниз. Кто первый положит орех в левую нижнюю клетку, тот выиграет. Первый ход делает рыжий бельчонок. Кто из бельчат всегда может выиграть?