Задача 1.
В прямоугольнике 6 × 6 некоторые клетки закрашены. Закрасьте ещё как можно меньше клеток, чтобы при сгибании квадрата по любой прямой из двух (см. рисунок) закрашенные клетки совмещались с закрашенными, а белые с белыми. Какое наибольшее число белых клеток останется?

Задача 2.
На факультативе занимается 9 четвероклассников. Им задали решить 6 задач. Все, кроме Саши и Вани, решили по 4 задачи. Каждую задачу решили 5 четвероклассников. Сколько задач решили вместе Саша и Ваня?
Задача 3.
Из мешка, в котором 7 кг кедровых орехов, надо отмерить в пакет ровно 1 кг. Как сделать это за три взвешивания, если можно использовать чашечные весы и одну гирю весом 600 г?
Задача 4.
Аня, Майя, и Люба принесли своих кошек делать прививку (каждая принесла одну кошку). Кошки у них разной породы: одна сибирская, другая сиамская, третья персидская. Девочки стали договариваться об очереди. Хозяйка сибирской кошки сказала: я первая не пойду. Хозяйка персидской кошки сказала: я пойду сразу после Ани. Хозяйка сиамской кошки сказала: если Майя не пойдёт второй, то я пойду сразу после Любы. Так они и сделали. В каком порядке заходили девочки, и какие у них кошки?
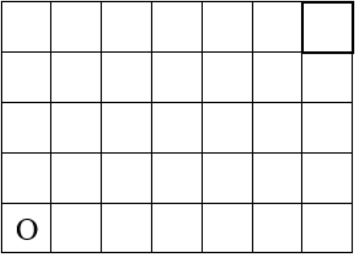
Задача 5.
Два бельчонка, рыжий и серый, играют в такую игру. Они начертили на земле прямоугольник 5 × 7 клеток, в левую нижнюю клетку положили орех (на рисунке он обозначен буквой О). За один ход можно переложить орех на любое количество клеток или вправо, или вверх. Кто первый положит орех в правую верхнюю клетку, тот выиграет. Первый ход делает рыжий бельчонок. Кто из бельчат всегда может выиграть?