Задача 5.
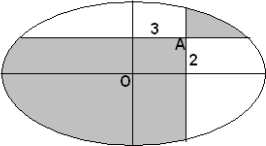
Миша хотел разрезать торт по осям симметрии (см. рисунок), но промахнулся, и провёл разрезы не через точку О, а через точку А, отстоящую от осей симметрии на 2 и на 3 сантиметра. На сколько площадь кусков, закрашенных серым, больше площади незакрашенных кусков?
Ответ на Задачу 5.
Ответ: 24 см2.
Решение:
Проведём вертикальную и горизонтальные прямые симметрично имеющимся прямым относительно центра О. Торт разобьётся на 16 кусков; пронумеруем их, как на рисунке.
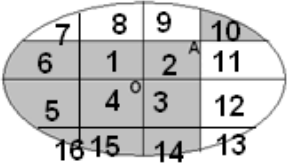
Площадь закрашенной области равна сумме площадей областей 1 + 2 + 3 + 4 + 5 + 6 + 10 + 14 + 15 + 16. Площадь белой области равна сумме площадей областей 7 + 3 + 9 + 11 + 12 + 13. По симметрии, площади некоторых областей равны: 1 = 2 = 3 = 4, 5 = 6 = 11 = 12, 7 = 10 = 13 = 16, 8 = 9 = 14 = 15.
Разность площадей закрашенной и белой областей равна:
1 + 2 + 3 + 4 + 5 + 6 + 10 + 14 + 15 + 16 − (7 + 8 + 9 + 11 + 12 + 13) = 1 + 2 + 3 + 4 = 4 ⋅ 6 = 24 см2.

