Задача 5.
Шесть команд провели турнир – каждая команда сыграла с каждой по разу. За ничью начислялось 1 очко, за проигрыш очков не давалось. Шесть команд набрали соответственно 10, 7, 6, 6, 3 и 3 очков. Сколько очков (не обязательно целое число) начислялось за победу?
Ответ на Задачу 5.
Ответ: 2,5 очка.
Решение:
Всего в турнире было сыграно 6 ⋅ 5 : 2 = 15 матчей.
Пусть за победу начислялось $x$ очков, было $k$ результативных встреч и $15 - k$ ничьих. Тогда суммарно команды набрали $xk + 2(15 - k)$ очков. По условию эта сумма равна 10 + 7 + 6 + 6 + 3 + 3 = 35, откуда $(x - 2)k = 5$. Следовательно, $x > 2$. Команда, набравшая 6 очков, выиграла хотя бы один матч, иначе она набрала бы не больше 5 очков. Из ограничения $x > 2$ следует, что она могла выиграть не более двух матчей. Значит, $x$ — целое или полуцелое число, в таком случае $k$ — делитель числа 10. С другой стороны, $k > 4$, поскольку у каждой из первых четырёх команд есть хотя бы одна победа. Следовательно, возможны только два варианта.
- $k = 5$, $x = 3$. Но в этом случае команда, набравшая 10 очков, должна была одержать ровно три победы, т.е. $k > 6$. Противоречие.
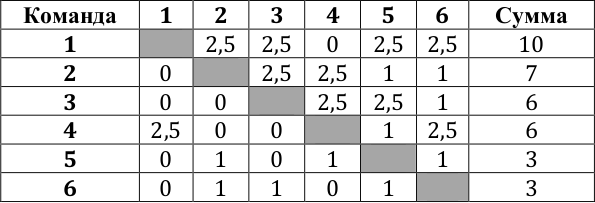
- $k = 10$, $x = 2,5$. Пример такого турнира приведён в таблице.