Задача 4.
Квадрат размером 100 × 100 клеток разбит на фигурки двух типов, изображённые на рисунке. Может ли оказаться, что фигурок из шести клеток ровно 333? Фигурки можно поворачивать и переворачивать.
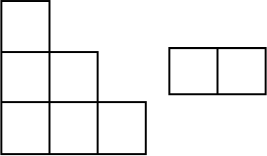
Ответ на Задачу 4.
Ответ: Не могла.
Решение:
Назовём первую фигурку — лесенкой. Рассмотрим шахматную раскраску нашей доски в два цвета — чёрный и белый. Тогда клеток чёрного и белого цветов будет одинаковое количество.
Заметим, что в каждом прямоугольнике 2 × 1 будет по одной чёрной и белой клетке. Это означает, что суммарно во всех лесенках количество клеток чёрного и белого цвета должно быть одинаковым. Но в каждой лесенке будет либо 4 белые и 2 чёрные клетки, либо 4 чёрные и 2 белые клетки.
Пусть х — количество лесенок первого вида, а у — второго вида. Тогда суммарное количество белых клеток в лесенках равно 4х + 2у, а чёрных — 2х + 4у. Отсюда следует, что 4х + 2у = 2х + 4у, т.е. х = у. Это означает, что общее количество лесенок 2х чётно и поэтому не может равняться 333.

