Задача 1.
Существует ли прямоугольный треугольник, гипотенуза которого численно равна половине его площади?
Задача 2.
Квадратный трёхчлен $p x^2 + q x + r$ имеет два корня. Докажите, что трёхчлен $3 p x^2 + 2(p + q) x + (q + r)$ также имеет два корня.
Задача 3.
Известно, что в трапеции $K L M N$ боковая сторона $K L$ равна основанию $L M$. Точки $P$ и $Q$ — середины оснований $K N$ и $L M$ соответственно, причём точка $P$ лежит на биссектрисе угла $L$. Докажите, что $L N = 2 P Q$.
Задача 4.
Квадрат размером 100 × 100 клеток разбит на фигурки двух типов, изображённые на рисунке. Может ли оказаться, что фигурок из шести клеток ровно 333? Фигурки можно поворачивать и переворачивать.
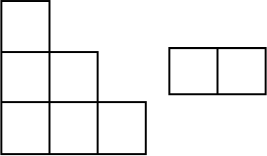
Задача 5.
Несколько команд провели турнир по гандболу — каждая команда сыграла с каждой по разу. За победу начислялось 2 очка, за ничью – 1 очко, за проигрыш очков не давалось. Если по итогам две команды набрали одинаковое число очков, более высокое место присуждалось команде, у которой больше разница между числом забитых и пропущенных мячей. Три команды, ставшие призёрами, набрали соответственно 7, 5 и 3 очков. Сколько очков набрала последняя команда?

