Задача 5.
Несколько команд провели турнир по гандболу — каждая команда сыграла с каждой по разу. За победу начислялось 2 очка, за ничью – 1 очко, за проигрыш очков не давалось. Если по итогам две команды набрали одинаковое число очков, более высокое место присуждалось команде, у которой больше разница между числом забитых и пропущенных мячей. Три команды, ставшие призёрами, набрали соответственно 7, 5 и 3 очков. Сколько очков набрала последняя команда?
Ответ на Задачу 5.
Ответ: 2 очка.
Решение:
Пусть в турнире участвовало $n$ команд, тогда было разыграно $n(n - 1)$ очков. Последние $n - 2$ команды (т.е. все, кроме занявших первые два места) набрали не более чем по 3 очка каждая. Значит, $n(n - 1) < 7 + 5 + 3(n – 2)$, откуда $n \le 5$.
Победившая команда набрала 7 очков, поэтому она провела не меньше четырёх игр. Следовательно, всего было 5 команд, которые разыграли между собой 5 ⋅ 4 = 20 очков.
Пусть четвёртая (по итогам чемпионата) команда набрала 𝑥 очков, а последняя — 𝑦 очков. Тогда общее число разыгранных очков равно 7 + 5 + 3 + 𝑥 + 𝑦 = 20, откуда следует, что 𝑥𝑦 = 5. Так как 𝑦 ≤ 𝑥 ≤ 3, получаем, что 𝑥 = 3, 𝑦 = 2. Значит, команда, занявшая последнее место, набрала 2 очка.
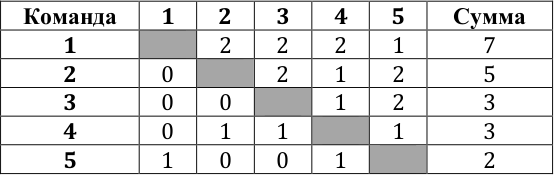
Пример турнира, удовлетворяющего условию задачи, приведён в таблице.