Олимпиада «Бельчонок», 8 класс, 2022 год, 2 этап, 4 вариант
дата проведения: 5 марта 2022
Задача 5.
Несколько команд провели турнир по хоккею — каждая команда сыграла с каждой по разу. За победу начислялось 2 очка, за ничью — 1 очко, за проигрыш очков не давалось. Команда «Бельчата» одержала больше всех побед и набрала меньше всех очков. Какое наименьшее количество команд могло принимать участие в турнире?
Ответ на Задачу 5.
Ответ: 6 команд.
Решение:
В турнире из $n$ команд «Бельчата» набрали меньше среднего количества, т.е. не больше $n - 2$ очков. Значит, какая-то команда набрала больше среднего, т.е. не меньше $n$ очков. Для этого ей пришлось одержать хотя бы одну победу. Следовательно, «Бельчата» одержали не меньше двух побед, т.е. набрала не меньше 4 очков. Поэтому $n > 6$.
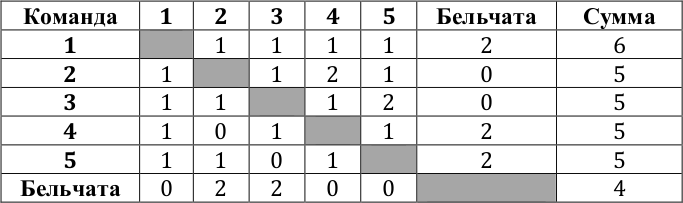
Пример для шести команд см. в таблице.