Задача 5.
Шесть команд провели турнир – каждая команда сыграла с каждой по разу. За ничью начислялось 1 очко, за проигрыш очков не давалось. Шесть команд набрали соответственно 12, 10, 9, 8, 7 и 6 очков. Сколько очков (не обязательно целое число) начислялось за победу?
Ответ на Задачу 5.
Ответ: 4 очка.
Решение:
Всего в турнире было сыграно 6 ⋅ 5 : 2 = 15 матчей.
Пусть за победу начислялось $x$ очков, было $k$ результативных встреч и $15 - k$ ничьих. Тогда суммарно команды набрали $xk + 2(15 - k)$ очков. По условию эта сумма равна 12 + 10 + 9 + 8 + 7 + 6 = 52, откуда $(x - 2)k = 22$. Тогда из ограничения $k \le 15$ получаем, что $x > 3$. Команда, занявшая последнее место, одержала хотя бы одну победу, иначе она набрала бы не больше 5 очков. Но так как $x > 3$, то и более одного матча она выиграть не могла, поэтому одержала ровно одну победу. Значит, за победу в матче начислялось целое число очков, причём не большее 6. Теперь из равенства $(x - 2)k = 22$ понятно, что $x = 4$.
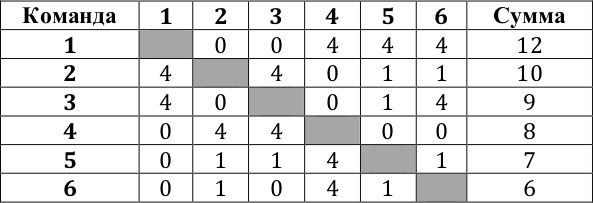
Пример турнира, удовлетворяющего условию, приведён в таблице.