Задача 1.
Софи рисует цветных кенгуру: сначала голубого, потом красного, потом чёрного, потом жёлтого, снова голубого, красного, чёрного, жёлтого и так далее. Какого цвета будет семнадцатый кенгуру?
(А) голубого
(Б) зелёного
(В) красного
(Г) чёрного
(Д) жёлтого
Задача 2.
Число 0 + 1 + 2 + 3 + 4 − 3 − 2 − 1 − 0 равно
(А) 0
(Б) 2
(В) 4
(Г) 10
(Д) 16
Задача 3.
На какой картинке сердечки составляют ровно три четверти от общего числа фигурок?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 4.
Если бы выходными днями в сентябре были все числа, в которых есть чётные цифры, то в школу в сентябре пришлось бы ходить
(А) 9 дней
(Б) 10 дней
(В) 11 дней
(Г) 12 дней
(Д) 15 дней
Задача 5.
Васиного отца зовут Иван Николаевич, а дедушку — Семён Петрович. Каково отчество Васиной мамы?
(А) Ивановна
(Б) Николаевна
(В) Семеновна
(Г) Петровна
(Д) Васильевна
Задача 6.
Лист бумаги сложили и разрезали, как показано на рисунке. Сколько кусочков получилось?
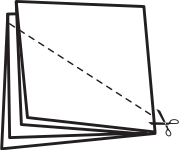
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 7.
Самое маленькое целое число, которое делится на 2, 3 и 4, равно
(А) 1
(Б) 2
(В) 6
(Г) 12
(Д) 24
Задача 8.
Пятачок посадил 8 желудей. Из всех желудей, кроме двух, выросли дубы. На всех дубах, кроме двух, растут жёлуди. Жёлуди со всех плодоносящих дубов, кроме одного, — невкусные. Значит, число дубов с невкусными желудями равно:
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 9.
В прямоугольнике 4 × 7, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала?
(А) 8
(Б) 9
(В) 10
(Г) 11
(Д) 12
Задача 10.
Выписав 6 чётных чисел, идущих подряд, Вася обнаружил, что самое большое из них вдвое больше самого маленького. Чему равно самое маленькое число?
(А) 4
(Б) 6
(В) 8
(Г) 10
(Д) 12
Задача 11.
Как-то в воскресенье, в 9 часов 30 минут утра, Аня присела поиграть в компьютерную игру, но заигралась, и мама прогнала её от компьютера только днём, в 15 часов 15 минут. В следующее воскресенье её брат Мартин ухитрился просидеть за компьютером ещё на 1 час 50 минут дольше. Сколько времени провёл у компьютера Мартин?
(А) 6 час 30 мин
(Б) 6 час 35 мин
(В) 7 час 35 мин
(Г) 10 час 15 мин
(Д) 3 часа
Задача 12.
Сколько треугольников на рисунке имеют такую же площадь, как и целая клетка?
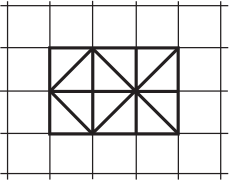
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) другой ответ
Задача 13.
На заседании присутствуют 29 академиков, 12 из них имеют бороду, а 18 — усы. У трёх академиков нет ни бороды, ни усов. Сколько академиков имеют и бороду, и усы?
(А) 4
(Б) 5
(В) 6
(Г) 11
(Д) 16
Задача 14.
Штрих-код образован 17 чёрными и белыми полосками (крайние полоски — чёрные). Черные полоски бывают двух типов: узкие и широкие. Число белых полосок на 3 больше, чем число широких чёрных. Чему равно число узких чёрных полосок?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 15.
Кенгуру купил конфеты трёх видов: большие, маленькие и средние. Каждая большая конфета стоит 4 монеты, средняя — 2 монеты и маленькая — 1 монету. За 10 конфет Кенгуру заплатил 16 монет. Сколько больших конфет он купил?
(А) 5
(Б) 4
(В) 3
(Г) 2
(Д) 1
Задача 16.
Чему равна площадь буквы N, если площадь клетки равна 1?
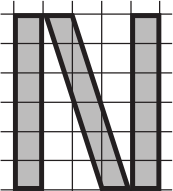
(А) 14
(Б) 15
(В) 16
(Г) 17
(Д) 18
Задача 17.
Серёжа любит подсчитывать сумму цифр на табло электронных часов. Например, если часы показывают 21:17, он получает сумму 11. Какую наибольшую сумму он может получить?
(А) 19
(Б) 23
(В) 24
(Г) 25
(Д) 36
Задача 18.
Сколько страниц в книжке, если для того, чтобы их пронумеровать, понадобилось всего 35 цифр?
(А) 17
(Б) 18
(В) 22
(Г) 24
(Д) 35
Задача 19.
Какое наибольшее число верёвочек можно разрезать на этой сетке, чтобы она не распалась на куски? (Разрезать по узелкам сетки нельзя!)

(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 11
Задача 20.
Во сколько раз увеличится трёхзначное число, если написать его два раза подряд?
(А) 2
(Б) 100
(В) 101
(Г) 1000
(Д) 1001
Задача 21.
Брусок собран из трёх деталей. Каждая деталь состоит из четырёх кубиков и окрашена в свой цвет. Как выглядит белая деталь?
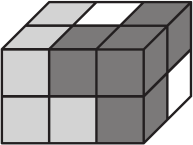
(А) 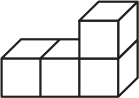
(Б) 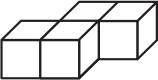
(В) 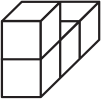
(Г) 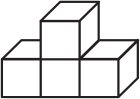
(Д) 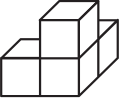
Задача 22.
Маша старше Миши ровно на один месяц (дни их рождения приходятся на одно и то же число в двух соседних месяцах), а Даша старше Миши на столько же дней, на сколько Маша старше Даши. В каком месяце не могла родиться Даша?
(А) в апреле
(Б) в мае
(В) в июле
(Г) в августе
(Д) в декабре
Задача 23.
В десятичной записи числа 79865 использованы 5 последовательных цифр. Чему равна третья цифра следующего пятизначного числа, обладающего таким же свойством?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) другой ответ
Задача 24.
После того, как из мозаики вынули две фигурки, составленные из её элементов, образовалась «дырка» (см. рисунок). Какие фигурки вынули?
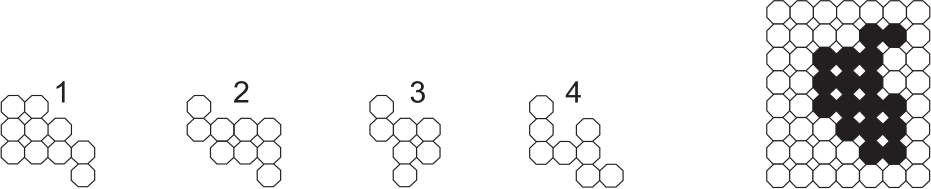
(А) 1 и 4
(Б) 2 и 4
(В) 2 и 3
(Г) 1 и 3
(Д) 3 и 4
Задача 25.
Вася изменяет число, написанное на доске, по следующему правилу: если это число делится на 3, то Вася вычитает из него 1; если число даёт остаток 2 при делении на 3, то Вася вычитает из него 2; а если число даёт остаток 1, то Вася прибавляет к нему 2. Он начинает с числа 10000. Какое число получит Вася после 2003 таких операций?
(А) 10000
(Б) 7004
(В) 7002
(Г) 6999
(Д) 3996
Задача 26.
Четыре девочки поют песни, аккомпанируя друг другу по очереди: каждый раз одна из них играет, остальные три поют. Оказалось, что Анна спела больше всех песен – восемь, а Дороти спела меньше всех – пять. Сколько всего песен спели девочки?
(А) 12
(Б) 11
(В) 10
(Г) 9
(Д) невозможно определить

