Задача 1.
Каждый из восьми кенгуру может перепрыгнуть на любую клетку квадратной таблицы 4 × 4. Им надо расположиться так, чтобы в каждой строчке и каждом столбце этой таблицы оказалось ровно по 2 кенгуру. Наименьшее число кенгуру, которым придётся для этого прыгнуть, равно:

(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 2.
Где ошибка?
(А) 2 + 0 + 0 + 5 = 5 + 0 + 0 + 2
(Б) 2 − (0 − 0 − 5) = 2 + (0 + 0) + 5
(В) 2 + 0 − 0 + 5 = 5 − 0 − 0 − 2
(Г) 2 + (0 + 0 + 5) = (2 + 0 + 0) + 5
(Д) (2 − 0) − (0 − 5) = (2 + 0) + (0 + 5)
Задача 3.
Вася делал домашнее задание по математике 1800 секунд, а потом утомился и пошёл гулять. Значит, над заданием по математике Вася сидел
(А) четверть часа
(Б) полчаса
(В) три четверти часа
(Г) два часа
(Д) три часа
Задача 4.
Муравей ползёт по поверхности кубика из точки А в точку В по пути, отмеченному стрелками. Чему равна длина этого пути, если ребро кубика равно 12 см?
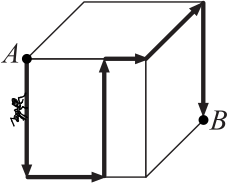
(А) 40 см
(Б) 48 см
(В) 50 см
(Г) 60 см
(Д) невозможно определить
Задача 5.
Чему равна цифра единиц двузначного числа, если известно, что она равна 3 / 8 от цифры десятков?
(А) 3
(Б) 5
(В) 8
(Г) 7
(Д) невозможно определить
Задача 6.
Пять карточек с цифрами лежат на столе в таком порядке: 1, 3, 5, 4, 2. За один ход разрешается поменять местами любые две карточки. За какое наименьшее число ходов можно расположить все карточки в порядке 1, 2, 3, 4, 5?
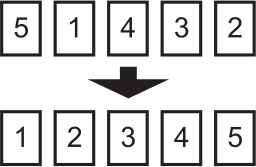
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 7.
Сколько часов во второй половине первой четверти суток?
(А) 1/3
(Б) 1/2
(В) 1
(Г) 2
(Д) 3
Задача 8.
Число 147∗2 делится на 7. Какая цифра зашифрована значком ∗?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 9.
На лесной опушке под каждой берёзой растёт по два подберёзовика, а на каждом пеньке — по 12 опят. Сколько берёз надо обойти, чтобы собрать столько же подберёзовиков, сколько опят растёт на 6 пеньках?
(А) 6
(Б) 12
(В) 18
(Г) 36
(Д) 72
Задача 10.
Какое из этих чисел является одновременно и кубом, и квадратом некоторых целых чисел?
(А) 8
(Б) 27
(В) 36
(Г) 64
(Д) 125
Задача 11.
Царь Кащей подобрел и решил потратить 50 золотых монет на подарки детям. В сундуке у него хранится 5 ларцов, в каждом ларце по 3 шкатулки, а в каждой шкатулке по 10 золотых монет. Сундук, ларцы и шкатулки заперты на замки. Какое наименьшее число замков потребуется открыть Кащею, чтобы достать 50 монет?
(А) 9
(Б) 8
(В) 7
(Г) 6
(Д) 5
Задача 12.
Квадратный листок разрезали на 3 части. Две из них изображены на рисунке ниже.

Какую форму может иметь третий кусок?
(А) 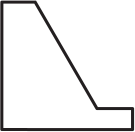
(Б) 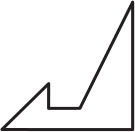
(В) 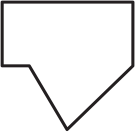
(Г) 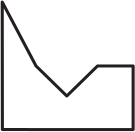
(Д) 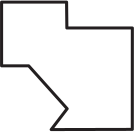
Задача 13.
Если число 2005 умножить само на себя 2005 раз, то последние две цифры произведения будут равны:
(А) 05
(Б) 15
(В) 25
(Г) 45
(Д) 7
Задача 14.
На рисунке изображены квадрат и 5 одинаковых касающихся кругов.
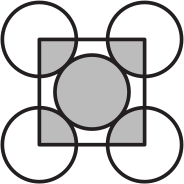
Площадь каждого из кругов равна 1. Вершины квадрата расположены в центрах внешних кругов. Тогда площадь закрашенной области равна:
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 15.
С полудня до полуночи Кот Ученый спит под дубом, а с полуночи до полудня рассказывает сказки. На дубе он повесил плакат: «Через час я буду делать то же самое, что делал два часа назад». Сколько часов в сутки эта надпись верна?
(А) 6
(Б) 12
(В) 18
(Г) 3
(Д) 21
Задача 16.
Если сумма трёх последовательных положительных целых чисел равна 99, то произведение цифр первого из них равно:
(А) 0
(Б) 3
(В) 6
(Г) 9
(Д) 12
Задача 17.
Каждый из двух согнутых кусков проволоки состоит из 8 участков длины 1. Один из кусков наложили на другой так, что они частично совпали. Какова наибольшая возможная длина их общей части?
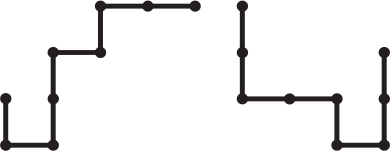
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 18.
Сумма числителя и знаменателя дроби равна 2005, а после сокращения этой дроби получилось число 400. Тогда сумма цифр числителя первоначальной дроби равна
(А) 1
(Б) 2
(В) 3
(Г) 5
(Д) 8
Задача 19.
На этой картинке можно увидеть треугольники и квадраты, причём квадратов меньше, чем треугольников. На сколько?
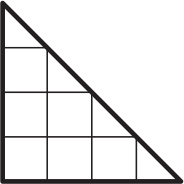
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) квадратов и треугольников поровну
Задача 20.
Получив очередную пятёрку по математике, Серёжа обнаружил, что в дневнике у него стало на 100% больше пятёрок, чем двоек. На сколько процентов количество двоек теперь меньше, чем количество пятёрок?
(А) на 0%
(Б) на 50%
(В) на 100%
(Г) на 150%
(Д) на 200%
Задача 21.
В классе сидят мальчики и девочки. Если в класс войдут ещё 10 мальчиков, то всего мальчиков станет вдвое больше, чем девочек. Сколько девочек должны выйти из класса, чтобы среди оставшихся ребят оказалось вдвое больше мальчиков, чем девочек?
(А) 0
(Б) 2
(В) 5
(Г) 10
(Д) 20
Задача 22.
Для украшения класса к празднику 8 Марта купили воздушные шарики: синие, красные и зелёные. Некоторые из них длинные, а некоторые – круглые. Все зелёные шарики – круглые, а все длинные – красные. Тогда обязательно
(А) все красные шарики – длинные
(Б) некоторые длинные шарики – синие
(В) все круглые шарики – зелёные
(Г) все синие шарики – круглые
(Д) некоторые синие шарики – длинные
Задача 23.
В произведении К × Е × Н × Г × У × Р × У буквами зашифрованы некоторые цифры (одинаковые цифры обозначены одинаковыми буквами, а разные – разными). Чему равна цифра единиц этого произведения, если известно, что оно не делится на 4?
(А) 0
(Б) 1
(В) 2
(Г) 5
(Д) невозможно определить
Задача 24.
На белой доске 5 × 5 Петя закрасил какие-то клетки синим цветом, а какие-то красным (каждым цветом закрашена хотя бы одна клетка). Никакие две клетки красного и синего цвета не имеют общей стороны. Какое наименьшее число клеток могло быть не закрашено?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 25.
Какую из фигурок можно склеить из заготовки, изображённой ниже?
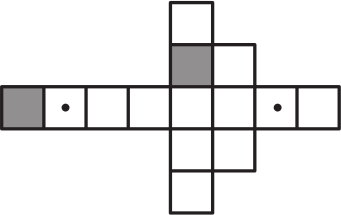
(А) 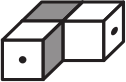
(Б) 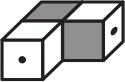
(В) 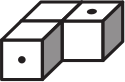
(Г) 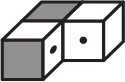
(Д) 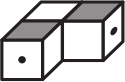
Задача 26.
В 3 часа Вася заметил, что стрелки часов образуют прямой угол, и стал ждать, когда это произойдёт в следующий раз. Сколько времени он ждал?
(А) 30 минут
(Б) 31 минуту
(В) 65 минут
(Г) 6/11 часа
(Д) 12/23 часа
Задача 27.
Сколько двузначных чисел обладают таким свойством: если переставить местами их цифры, то они увеличиваются не менее, чем в 3 раза?
(А) 5
(Б) 6
(В) 10
(Г) 15
(Д) 33
Задача 28.
Катя и четыре её подружки разделили между собой несколько конфет. В результате оказалось, что у всех девочек разное число конфет, а общее число конфет у любых трёх девочек больше, чем общее число конфет у остальных двух. Какое самое маленькое число конфет может быть у Кати?
(А) 1
(Б) 2
(В) 4
(Г) 5
(Д) 7
Задача 29.
Гусеница выползла из своего домика в полдень и ползёт по лугу, поворачивая после каждого часа направо или налево на 90º. За первый час она проползла 1 м, а за каждый следующий — на 1 м больше, чем за предыдущий. На каком наименьшем расстоянии от домика она могла оказаться в 7 часов вечера?
(А) 0 м
(Б) 1 м
(В) 2 м
(Г) 5 м
(Д) 9 м
Задача 30.
Яблоко и апельсин вместе весят столько же, сколько груша и персик. Яблоко вместе с грушей весят меньше, чем апельсин с персиком, а груша вместе с апельсином весят меньше, чем яблоко с персиком. Какой из фруктов самый тяжёлый?
(А) апельсин
(Б) персик
(В) груша
(Г) яблоко
(Д) невозможно определить

