Задача 1.
В каком месяце у Кенгуру день рождения, если ровно через полгода после этого дня он сказал: «Два месяца назад был конкурс «Кенгуру»?
(А) в сентябре
(Б) в октябре
(В) в ноябре
(Г) в январе
(Д) в мае
Задача 2.
Точка O – центр правильного пятиугольника. Какая часть площади закрашена?
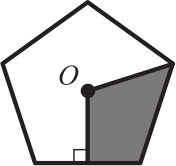
(А) 10%
(Б) 20%
(В) 25%
(Г) 30%
(Д) 40%
Задача 3.
Бабушка сказала внукам: «Если я испеку каждому из вас по два пирожка, у меня останется теста на три лишних пирожка, а если я захочу испечь каждому из вас по три пирожка, то мне не хватит теста на два пирожка». Сколько внуков у бабушки?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 4.
Из какой из следующих разверток можно склеить изображённый кубик?
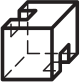
(А) 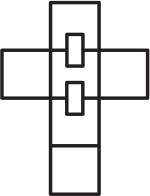
(Б) 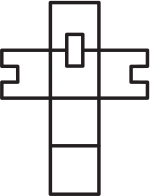
(В) 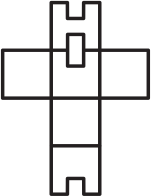
(Г) 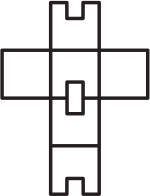
(Д) 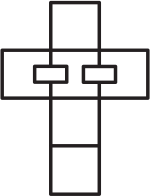
Задача 5.
Если x : y = 5, y : z = 4, u : z = 4 и v : u = 3, то чему равно x : v ?
(А) 3
(Б) 4
(В) 5
(Г) 3/5
(Д) 5/3
Задача 6.
Один лилипут весит один миллипуд, а Гулливер весит 100 кг. Зная, что пуд — это 16 килограммов, определите, сколько лилипутов весят столько же, сколько и Гулливер.
(А) 625
(Б) 1600
(В) 6250
(Г) 16000
(Д) 62500
Задача 7.
Фигура на картинке сложена из двух кубиков. Ребро меньшего кубика — 1 см, а ребро большего — 3 см. Какова площадь поверхности этой фигуры?
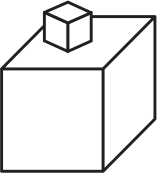
(А) 56 см2
(Б) 58 см2
(В) 60 см2
(Г) 62 см2
(Д) 64 см2
Задача 8.
Коты Тоша и Малыш едят из одной плошки. Первым подбегает Малыш и съедает треть всей еды. Потом Тоша съедает половину того, что осталось. После этого Малыш съедает треть того, что осталось, и так далее. За день каждый из котов ест 5 раз. Тогда к концу дня
(А) Малыш съест больше Тоши
(Б) коты съедят поровну
(В) Тоша съест в три раза больше
(Г) еда кончится
(Д) Тоша съест в полтора раза больше
Задача 9.
Какое число расположено ровно посередине между числами $\displaystyle \frac{1}{8}$ и $\displaystyle \frac{1}{10}?$
(А) $\displaystyle \frac{1}{80}$
(Б) $\displaystyle \frac{1}{40}$
(В) $\displaystyle \frac{1}{18}$
(Г) $\displaystyle \frac{1}{9}$
(Д) $\displaystyle \frac{9}{80}$
Задача 10.
Найдите наибольший возможный периметр равнобедренного треугольника, если длина его боковой стороны — 7 см, а длина основания равна целому числу сантиметров.
(А) 14 см
(Б) 15 см
(В) 21 см
(Г) 27 см
(Д) 28 см
Задача 11.
Если он синий, то он круглый. Если он квадратный, то он красный. Он либо синий, либо жёлтый. Если он жёлтый, то он квадратный. Он либо квадратный, либо круглый. Тогда:
(А) он красный и квадратный
(Б) он красный и круглый
(В) он синий и квадратный
(Г) он синий и круглый
(Д) он жёлтый и круглый
Задача 12.
Сколько процентов от 5% от числа a составляет столько же, сколько 8% от 3% от числа 2a ?
(А) 9,6%
(Б) 2,4%
(В) 6%
(Г) 4,8%
(Д) другой ответ
Задача 13.
В классе 21 ученик. Известно, что ни у каких двух девочек количество друзей-мальчиков из этого класса не совпадает. Какое наибольшее количество девочек может быть в этом классе?
(А) 5
(Б) 6
(В) 9
(Г) 11
(Д) 15
Задача 14.
Прямоугольник на рисунке составлен из 7 квадратов. Сторона каждого закрашенного квадрата равна 8. Чему равна сторона большого белого квадрата?
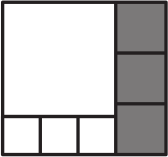
(А) 15
(Б) 18
(В) 20
(Г) 24
(Д) 30
Задача 15.
Часы Остапа Бендера испортились, и теперь у них часовая и минутная стрелки поменялись ролями. Ровно в полночь Остап поставил на своих часах точное время. Сколько раз за период от 00:01 до 23:59 в предстоящие сутки эти часы покажут правильное время?
(А) ни разу
(Б) 2 раза
(В) 11 раз
(Г) 21 раз
(Д) 23 раза
Задача 16.
Найдите наибольшее возможное количество цифр числа, обладающего следующим свойством: если закрыть все его цифры, кроме двух соседних, то всегда будет получаться квадрат натурального числа.
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 17.
Если прямые у = 2х + 3 и у = −х + b пересекаются в первой четверти, то:
(А) b < −3
(Б) −3 < b < −1
(В) −1 < b < 2
(Г) 2 < b < 3
(Д) b > 3
Задача 18.
Жан-Кристоф продолжает изучать русский язык. На этот раз он выписывает словами все трёхзначные числа, в десятичной записи которых участвует ноль и ещё две одинаковые цифры. Каждый раз получается два слова. У скольких чисел эти два слова начинаются с разных букв?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) больше 3
Задача 19.
Про a и b известно, что a + b > 0 и a + 2b < 0. Какое из следующих выражений может принимать как положительные, так и отрицательные значения?
(А) a
(Б) b
(В) 2a + b
(Г) 2a + 3b
(Д) a + 3b
Задача 20.
Прямая разрезает пятиугольник (не обязательно выпуклый) на несколько частей. Тогда ни одна из получившихся частей не может быть:
(А) треугольником
(Б) пятиугольником
(В) шестиугольником
(Г) семиугольником
(Д) все фигуры А-Г могут получиться
Задача 21.
Петер едет на своём велосипеде из точки P в точку Q с постоянной скоростью. Если бы он увеличил скорость на 3 м/с, то он доехал бы до Q в три раза быстрее. Во сколько раз быстрее он доехал бы до Q, увеличив скорость на 6 м/с?
(А) 4
(Б) 5
(В) 6
(Г) 4,5
(Д) 8
Задача 22.
Если O — центр окружности, OR = QP и ∠AOR = 60º, то угол ∠RPO равен:
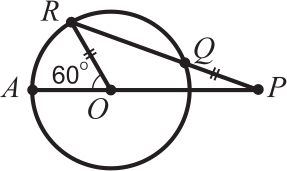
(А) 15º
(Б) 20º
(В) 22,5º
(Г) 30º
(Д) 45º
Задача 23.
Пусть A(n) – это число, которое получается, если выписать подряд все натуральные числа от 1 до n. Например, А(11) = 1234567891011. Назовем число n «богатым», если в записи числа А(n) встречается набор подряд идущих цифр 4321. Если N — самое маленькое из «богатых» чисел, то:
(А) N < 1000
(Б) 1000 < N < 2000
(В) 2000 < N < 3000
(Г) 3000 < N < 4000
(Д) N > 4000
Задача 24.
Сумма трёх положительных чисел равна 20. Тогда произведение двух бóльших из них не может быть
(А) больше 99
(Б) меньше 0,001
(В) равно 75
(Г) равно 25
(Д) все случаи А-Г возможны.
Задача 25.
Какое из равенств может быть неверным, если $a^3 = a + 1$ ?
(А) $a^4 = a^2 + a$
(Б) $a^4 = a^3 + a^2 − 1$
(В) $a^4 = a^5 − 1$
(Г) $\displaystyle a^2 + a = \frac{1}{a − 1}$
(Д) $a^5 = a^4 − 1$
Задача 26.
Две стороны четырёхугольника равны 1 и 4, а одна из диагоналей имеет длину 2 и делит этот четырёхугольник на два равнобедренных треугольника. Чему равен периметр такого четырёхугольника?
(А) 10
(Б) 11
(В) 12
(Г) 13
(Д) 14
Задача 27.
На доске выписаны числа от 1 до 2006. Вася подчеркнул все числа, делящиеся на 2, затем все числа, делящиеся на 3, а затем все числа, делящиеся на 4. Сколько чисел подчёркнуто ровно два раза?
(А) 1003
(Б) 1002
(В) 501
(Г) 334
(Д) 167
Задача 28.
На какую наибольшую степень числа 2 делится число 102005 − 22005 ?
(А) 2004
(Б) 2005
(В) 2006
(Г) 2007
(Д) 2008
Задача 29.
На заседании международного жюри конкурса «Кенгуру» за круглым столом сидят 12 человек. При этом на любых шести последовательных местах сидят представители не более, чем трёх разных стран. Представители какого наибольшего количества стран могут сидеть за столом?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 30.
Произведение двух натуральных чисел равно 24 ⋅ 32 ⋅ 5 ⋅ 73 ⋅ 11. Тогда их сумма может
(А) делиться на 5
(Б) делиться на 49
(В) делиться на 9
(Г) делиться на 8
(Д) ни одно из свойств А-Г невозможно

