Задача 1.
Конкурс «Кенгуру» всегда проходит в третий четверг марта. Самый ранний из возможных дней для проведения «Кенгуру» — это
(А) 10 марта
(Б) 12 марта
(В) 15 марта
(Г) 19 марта
(Д) 20 марта
Задача 2.
Сколько кусков верёвки изображено на рисунке?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 3.
Какая из этих дробей не равна $\displaystyle \frac{1}{3}$ ?
(А) $\displaystyle \frac{2}{6}$
(Б) $\displaystyle \frac{3}{9}$
(В) $\displaystyle \frac{4}{12}$
(Г) $\displaystyle \frac{5}{15}$
(Д) $\displaystyle \frac{6}{24}$
Задача 4.
День рождения Андрея — 25 февраля. Какой это по счёту день года?
(А) 55
(Б) 56
(В) 57
(Г) 58
(Д) 59
Задача 5.
В комнате сидят несколько кошек и собак. Кошачьих лап в комнате вдвое больше, чем собачьих носов. Тогда кошек в комнате
(А) вдвое меньше, чем собак
(Б) столько же, сколько собак
(В) вдвое больше, чем собак
(Г) в 4 раза меньше, чем собак
(Д) в 4 раза больше, чем собак
Задача 6.
На рисунке изображён прямоугольник, составленный из квадратов трёх разных размеров. Длина стороны самого маленького квадрата равна 1. Чему равна длина выделенной линии?
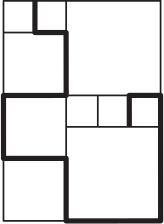
(А) 19
(Б) 20
(В) 21
(Г) 22
(Д) 23
Задача 7.
У Саши есть два одинаковых белых и два одинаковых красных кубика. Сколько различных башенок высотой в 3 кубика он может построить?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 8.
Через реку шириной 120 метров построен мост. Одна четверть длины моста расположена над левым берегом, одна четверть — над правым берегом. Чему равна длина моста?
(А) 150 м
(Б) 180 м
(В) 210 м
(Г) 240 м
(Д) 270 м
Задача 9.
В слове КЕНГУРУ поменяли местами две соседние буквы, в полученном «слове» проделали то же самое. Что не могло получиться?
(А) КЕНУГУР
(Б) КЕНГУРУ
(В) ЕНКГУРУ
(Г) КНЕГУУР
(Д) КУНЕГУР
Задача 10.
На столе стоят три ящика: белый, красный и зелёный. В одном лежат шоколадки, в другом яблоки, а третий пуст. Шоколадки лежат либо в белом, либо в красном ящике, а яблоки не лежат ни в белом, ни в зелёном ящике. Где лежат шоколадки?
(А) в белом ящике
(Б) в красном ящике
(В) в зелёном ящике
(Г) в красном или в зелёном ящике
(Д) невозможно определить
Задача 11.
В школе танцев сначала занималось 60 мальчиков и 20 девочек. Каждую неделю в школу приходит три новых девочки, а два мальчика бросают занятия. Сколько учеников будет в этой школе, когда число мальчиков и девочек сравняется?
(А) 90
(Б) 88
(В) 80
(Г) 72
(Д) 60
Задача 12.
Изображенная на рисунке башня состоит из равностороннего треугольника, прямоугольника и квадрата. Сторона квадрата равна 9 см, и периметры всех трёх фигур одинаковы. Чему равна меньшая сторона прямоугольника?
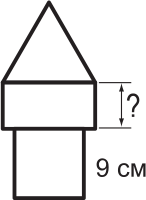
(А) 4 см
(Б) 5 см
(В) 6 см
(Г) 7 см
(Д) 8 см
Задача 13.
Серёжа очень любит поспать, и спит не меньше 10 часов в сутки. Сейчас ему 10 лет. Сколько часов он мог проспать за все эти годы?
(А) 15 000
(Б) 25 000
(В) 36 000
(Г) 40 000
(Д) 100 000
Задача 14.
Владелец маленького магазинчика заплатил 1000 рублей за упаковку авторучек. Когда он продал две трети этих авторучек, то вернул три четверти денег, затраченных на их покупку. Сколько денег он получит, продав всю упаковку?
(А) 1250 руб.
(Б) 1125 руб.
(В) 1000 руб.
(Г) 900 руб.
(Д) 750 руб.
Задача 15.
Через 7 часов наверняка уже будет «завтра». Сколько часов назад наверняка было «вчера»?
(А) 10
(Б) 15
(В) 20
(Г) 25
(Д) 45
Задача 16.
Если в числе 12323314 стереть несколько цифр, то можно получить число, которое будет читаться одинаково справа налево и слева направо. Наименьшее количество цифр, которые придётся для этого стереть, равно
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 17.
Коробка имеет размеры 30 × 30 × 50. Самое маленькое число кубиков одинакового размера, которыми можно заполнить эту коробку, равно
(А) 45
(Б) 90
(В) 120
(Г) 450
(Д) 45000
Задача 18.
На числовой прямой отмечены точки, изображающие числа 1/4 и 2/3 . Какая из точек P, Q, R и S изображает число 1/2 ?
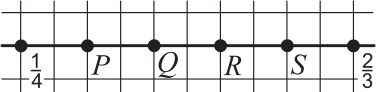
(А) P
(Б) Q
(В) R
(Г) S
(Д) другая точка
Задача 19.
Сколько существует способов выбрать три числа из набора 1, 2, 3, 4, 5, 6, 7 и 8 так, чтобы сумма выбранных чисел равнялась сумме оставшихся чисел?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 20.
В стране Смешляндии у каждого жителя левая нога на один или два размера больше, чем правая, хотя в магазинах обувь продаётся парами одного размера. Компания друзей решила сэкономить и купить туфли вместе. В результате каждый из них получил пару подходящей обуви, и ещё остались один башмак 45 размера и один башмак 36 размера. Самое маленькое число друзей, из которых могла состоять такая компания, равно
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 21.
В углах квадрата 10 × 10 вырезали маленькие квадратики 2 × 2. Чему равна площадь закрашенной области?

(А) 40
(Б) 42
(В) 48
(Г) 52
(Д) 64
Задача 22.
Таблица состоит из двух столбцов. В каждой строке, начиная со второй, записаны сумма и разность чисел предыдущей строки (всегда из большего числа вычитают меньшее). Чему равна сумма чисел в первой строке этой таблицы, если в седьмой строке стоят числа 96 и 64?
(А) 20
(Б) 18
(В) 16
(Г) 12
(Д) 8
Задача 23.
Два различных трёхзначных числа назовём родственниками, если они записаны одинаковыми тройками цифр. Например, 244 и 424 — родственники. Какое наименьшее количество родственников может иметь число с суммой цифр 10?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 6
Задача 24.
Фома, герой стихотворения С. Михалкова, не верил никогда и ничему. Однажды мама ему сказала: «Завтра не будет дождя, или папа отвезет тебя в школу на машине». Что должен сделать Фома следующим утром, если он, как обычно, не поверил тому, что сказала мама?
(А) раскрыть зонт и сесть в машину
(Б) раскрыть зонт и пойти пешком
(В) пойти в школу пешком без зонта
(Г) сесть в машину без зонта
(Д) ничего из перечисленного
Задача 25.
Оливер рисует на клетчатой бумаге прямоугольники, состоящие из 2009 клеточек, и вычисляет их периметры. Сколько разных результатов он может получить?
(А) 1
(Б) 2
(В) 3
(Г) 5
(Д) 10
Задача 26.
«Бабочка» — это фигура, составленная из четырёх отрезков, два из которых пересекаются (такая, как на рисунке). Проведем на этом рисунке ещё один отрезок. Какое наибольшее число «бабочек» может оказаться на полученном чертеже?

(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 27.
В числовом ребусе KANG − AROO = 2009 разные буквы обозначают разные цифры. Какая цифра обозначена буквой N?
(А) 4
(Б) 3
(В) 2
(Г) 1
(Д) 0
Задача 28.
Дикарь Пятница написал в строчку несколько различных натуральных чисел, не превосходящих 10. Робинзон Крузо заметил, что в любой паре соседних чисел одно из них делится на другое. Какое наибольшее количество чисел мог выписать Пятница?
(А) 6
(Б) 7
(В) 8
(Г) 9
(Д) 10
Задача 29.
Среди чисел 200, 201, …, 400 ровно два делятся на n. Какое наибольшее количество среди тех же чисел может делиться на n + 1?
(А) 4
(Б) 3
(В) 2
(Г) 1
(Д) 0
Задача 30.
Три стрелочки, изображённые на рисунке, соединяют некоторые из 9 точек, отмеченных на клетчатой бумаге. При этом ни одна стрелочка не идёт по границе клетки, а в каждой строчке и в каждом столбце начинается ровно одна стрелочка и заканчивается ровно одна стрелочка. Сколько всего троек стрелочек с такими свойствами можно провести?
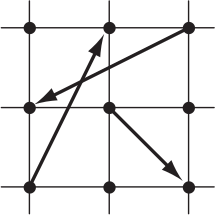
(А) 4
(Б) 8
(В) 12
(Г) 24
(Д) 36

