Задача 1.
В 2009 году в конкурсе «Кенгуру» приняли участие 5,5 миллионов ребят из 46 стран. Каждый из них заполнил бланк ответов. Если один бланк весит 3 грамма, то все эти бланки вместе весят
(А) 165 тонн
(Б) 16,5 тонн
(В) 1,65 тонны
(Г) 165 кг
(Д) 16,5 кг
Задача 2.
Какая цифра зашифрована значком  , если
, если  +
+  + 6 =
+ 6 =  +
+  +
+  +
+  ?
?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 3.
У мухи 6 лапок, а у паука — 8. Два паука и две мухи вместе имеют столько же лапок, сколько 10 птичек и
(А) 2 кошки
(Б) 3 мышки
(В) 4 белки
(Г) 5 зайцев
(Д) 6 собак
Задача 4.
На рисунке показано, как цифра 4 отражается в двух зеркалах. Что будет видно на месте знака вопроса, если то же самое сделать с цифрой 5?
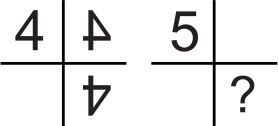
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 5.
На столе в ряд выложено 23 конфеты. Ник и Майк считают эти конфеты: один справа налево, а другой — слева направо. Какой номер даст Майк той конфете, которую Ник назвал одиннадцатой?
(А) 11
(Б) 12
(В) 13
(Г) 14
(Д) 15
Задача 6.
Сторона клеточки равна 1 см. Сколько различных путей длины 8 см, идущих по сторонам клеточек, ведёт из точки А в точку В?
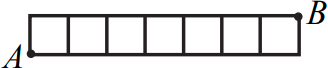
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 7.
Бен выбрал число, разделил его на 7, затем прибавил 7, а после этого результат умножил на 7. Получилось число 77. Какое число Бен выбрал?
(А) 7
(Б) 11
(В) 17
(Г) 28
(Д) 77
Задача 8.
Какой самый маленький результат можно получить, вставив пару скобок в выражение 2010 : 10 + 2010 : 201 + 2010 ⋅ 0 ?
(А) 2010
(Б) 201
(В) 211
(Г) 100,5
(Д) 0
Задача 9.
Что получится, если фигурку, изображённую ниже, повернуть на пол-оборота?

(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 10.
Какое из следующих чисел нечётно, если a и b — нечётные числа?
(А) a + b
(Б) ab
(В) a − b
(Г) 2a + 2b
(Д) 2ab
Задача 11.
Чему равно число 1 : (2 : (3 : 4)) ?
(А) 1/24
(Б) 1/12
(В) 3/8
(Г) 2/3
(Д) 4/3
Задача 12.
Числа 1, 4, 7, 10 и 13 требуется вписать в клеточки фигуры, изображённой ниже. При этом сумма чисел в трёх клеточках, расположенных по вертикали, должна равняться сумме чисел в трёх клеточках, расположенных по горизонтали. Какое самое большое значение может иметь эта сумма?
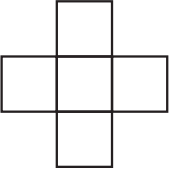
(А) 12
(Б) 18
(В) 21
(Г) 24
(Д) 35
Задача 13.
Заменяя в выражении 2 ∗ 0 ∗ 1 ∗ 0 = 1 каждую из звёздочек либо на «+», либо на «−», можно получить различные равенства. Сколько среди них правильных?
(А) 5
(Б) 4
(В) 3
(Г) 2
(Д) 1
Задача 14.
Чему равна площадь закрашенной области, если сторона квадрата равна 6 см, а x = 2 см?
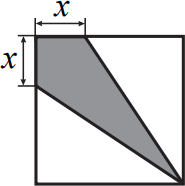
(А) 24 см2
(Б) 12 см2
(В) 6 см2
(Г) 4 см2
(Д) 3 см2
Задача 15.
Для каждой пары различных чисел из списка 1, 2, 3, …, 2010 робот находит их сумму. Сколько различных результатов он получит?
(А) 4020
(Б) 4019
(В) 4018
(Г) 4017
(Д) 2010
Задача 16.
Сколько из чисел 2010, 20100, 2010020, 201002010, 2010020100 делится на 12?
(А) 5
(Б) 4
(В) 3
(Г) 2
(Д) 1
Задача 17.
Три одинаковых игральных кубика склеены вместе. Общее количество точек на любых двух противоположных гранях кубика равно 7. Сколько всего точек нарисовано на склеенных гранях?
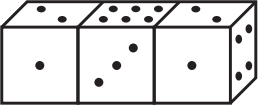
(А) 12
(Б) 13
(В) 14
(Г) 15
(Д) 16
Задача 18.
Конструкция на рисунке весит 112 граммов и находится в равновесии (вес горизонтальных планок и вертикальных нитей не учитывается). Сколько весит звёздочка?
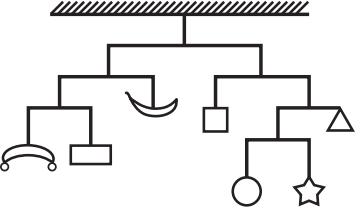
(А) 6 г
(Б) 7 г
(В) 12 г
(Г) 16 г
(Д) невозможно определить
Задача 19.
Саша и его папа собирали грибы. Саша нашёл на 18 грибов больше, чем половина грибов, найденных папой. Папа нашёл на 7 грибов больше, чем Саша. Сколько грибов нашли Саша и папа вместе?
(А) 93
(Б) 88
(В) 70
(Г) 61
(Д) 50
Задача 20.
Андрей обмотал веревочкой плоскую пластинку, изображённую справа. Как может выглядеть эта пластинка с противоположной стороны?
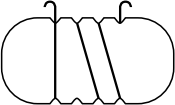
(А)
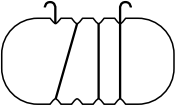
(Б)
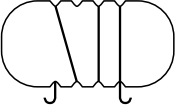
(В)
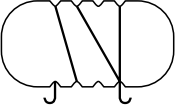
(Г)
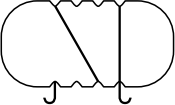
(Д)
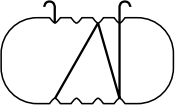
Задача 21.
Какое число закрашенных клеточек надо сделать белыми, чтобы в каждой колонке и каждой строке осталось ровно по одной закрашенной клетке?

(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) это невозможно сделать
Задача 22.
Газету из 60 страниц печатают на 15 листах бумаги (по две страницы на каждой стороне листа). Листы складывают в стопку, затем вместе сгибают пополам и нумеруют полученные страницы подряд числами от 1 до 60. Если из такой газеты потерялся лист со страницей номер 7, каких ещё страниц в ней не окажется?
(А) 6, 53 и 54
(Б) 8, 42 и 43
(В) 8, 48 и 49
(Г) 8, 52 и 53
(Д) 8, 53 и 54
Задача 23.
Шестиногие, семиногие и восьминогие кальмары служат подводному королю. Семиногие кальмары всегда лгут, а остальные всегда говорят правду. Однажды встретились 4 кальмара. Синий кальмар сказал: «Вместе у нас 28 ног», зелёный сказал: «Вместе у нас 27 ног», жёлтый сказал «Вместе у нас 26 ног», а красный сказал: «Вместе у нас 25 ног». Какой из кальмаров сказал правду?
(А) красный
(Б) синий
(В) зелёный
(Г) жёлтый
(Д) все кальмары солгали
Задача 24.
В числовом ребусе буквы P, Q и R обозначают различные цифры. Чему равна сумма P + Q + R ?
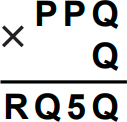
(А) 13
(Б) 15
(В) 16
(Г) 17
(Д) 20
Задача 25.
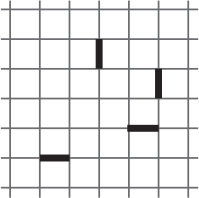
Из листа клетчатой бумаги Маша вырезала кусок, состоящий из целых клеточек. Она резала по сторонам клеточек, причём четыре отрезка, отмеченных на рисунке, оказались на границе вырезанного куска. Из какого наименьшего количества клеточек мог состоять этот кусок?
(А) 7
(Б) 8
(В) 9
(Г) 11
(Д) 13
Задача 26.
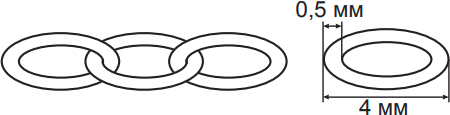
Ювелир изготавливает цепь из одинаковых звеньев (см. рисунки). Какую длину будет иметь цепь из 5 звеньев?
(А) 20 мм
(Б) 19 мм
(В) 17,5 мм
(Г) 16 мм
(Д) 15 мм
Задача 27.
Какой цифрой оканчивается самое маленькое число, у которого произведение цифр равно 2000?
(А) 0
(Б) 2
(В) 4
(Г) 5
(Д) 8
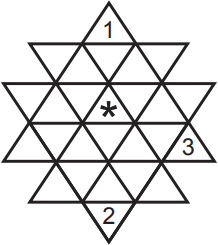
Задача 28.
В каждый маленький треугольник надо вписать одно из чисел 1, 2, 3, 4. Вписывать надо так, чтобы в любой полоске, состоящей из 4 маленьких треугольников, встречались все 4 числа. Некоторые числа уже вписаны. Какое число может быть вписано вместо ∗ ?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) так вписать числа нельзя
Задача 29.
В доме 20 квартир с номерами от 1 до 20 (сумма всех этих номеров равна 210). Однажды шутники заменили часть табличек с номерами квартир на другие (из этого же списка). В результате сумма всех номеров стала равной 135. Какое самое маленькое число номеров могло быть заменено?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 30.
На клетчатой доске 4 × 4 есть 4 горизонтальных ряда клеток, 4 вертикальных и 10 диагональных рядов (угловые клетки рядов не образуют). На этой доске отметили 10 клеток так, что число рядов с чётным количеством отмеченных клеток оказалось самым большим из возможных (0 — число чётное!). Чему равно это число рядов?
(А) 18
(Б) 17
(В) 16
(Г) 14
(Д) 12

