Задача 23.
Вася хочет вписать числа от 1 до 7 в вершины семиугольника. В каждый круг можно вписать только одно число. Он хочет, чтобы сумма чисел в двух соседних кругах равнялась числу, написанному на ребре, которое их соединяет. Какое число Вася должен вписать в закрашенный круг?
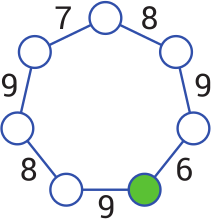
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Ответ на Задачу 23.
Ответ: Г
Решение:
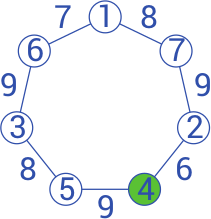
Обратим внимание, что число 1 не может стоять в круге, соединённым ребром, на котором написано число 9, так как 9 − 1 = 8, а Вася вписывает цифры от 1 до 7. Единственная позиция, куда можно поставить 1 – это самый верхний круг. Все последующие цифры, расположенные в кругах, вычисляются путём вычитания числа на ребре и предыдущей найденной цифры в круге. 8 − 1 = 7, 9 − 7 = 2 и т.д. Таким образом находим, что в закрашенном круге находится число 4.

