Задача 15.
На рисунке изображены два больших квадрата, площади которых равны. Часть каждого из квадратов закрашена, как показано на рисунке.
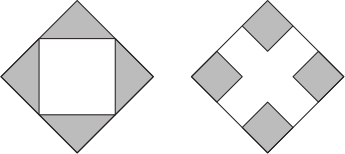
В первом квадрате отрезками соединены середины соседних сторон. Во втором квадрате закрашены четыре квадрата меньшего размера, длины сторон которых равны трети длины стороны большого квадрата. Площадь закрашенной части в первом квадрате равна 9. Чему равна площадь закрашенной части во втором квадрате?
(А) 4
(Б) 8
(В) 9
(Г) 10
(Д) 12
Ответ на Задачу 15.
Ответ: Б
Решение:
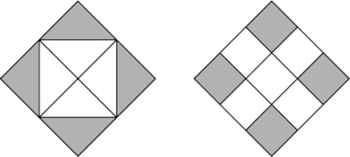
Квадрат слева можно разделить на четыре одинаковых квадрата меньшего размера (см. рисунок). В каждом из этих маленьких квадратов заштрихована половина квадрата. Итак, площадь большого квадрата равна 9 ⋅ 2 = 18. Квадрат справа можно разделить на 9 одинаковых квадратов. Четыре из них заштрихованы, поэтому общая заштрихованная площадь квадрата справа равна 18 : 9 ⋅ 4 = 8.

