Задача 1.
Алина складывает лист бумаги с картинкой по пунктирной линии:
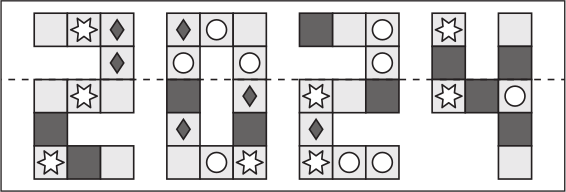
Какой из следующих квадратов наложится на точно такой же квадрат?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 2.
На рисунке показаны несколько первых движений игры в прыжки. Последовательность изображений повторяется каждые четыре клетки. Мила прыгает, приземляясь на ноги так, как нарисовано в каждой клетке. В какой из следующих клеток Мила приземлится только на правую ногу?

(А) в 10-й
(Б) в 15-й
(В) в 20-й
(Г) в 22-й
(Д) в 23-й
Задача 3.
Саша придумал секретный алфавит. Он записал слово ПИРОГ как  , а слово НАШ как
, а слово НАШ как 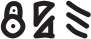 . Как он запишет слово ШПИОН?
. Как он запишет слово ШПИОН?
(А) 
(Б) 
(В) 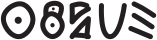
(Г) 
(Д) 
Задача 4.
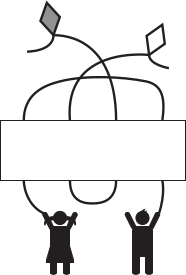
Какое изображение должно стоять вместо белого прямоугольника, чтобы получилась картинка, на которой каждый ребёнок держит своего воздушного змея?
(А) 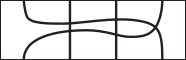
(Б) 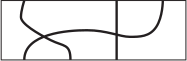
(В) 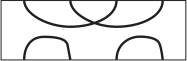
(Г) 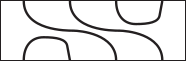
(Д) 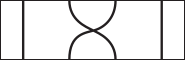
Задача 5.
Дина поставила три бруска на пол, а затем поставила перед ними белый кирпич. Когда она смотрит спереди, конструкция выглядит так, как показано на рисунке справа. Как выглядит эта конструкция с обратной стороны?
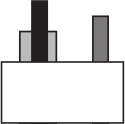
(А) 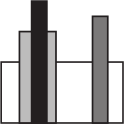
(Б) 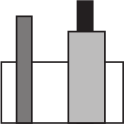
(В) 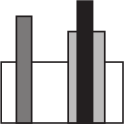
(Г) 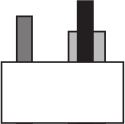
(Д) 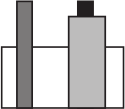
Задача 6.
На рисунке изображена фигура из трёх отрезков с указанными длинами. Маша хочет нарисовать эту фигуру, не отрывая карандаш от бумаги. Какова длина наименьшего пути, который Маша должна провести, чтобы это сделать?
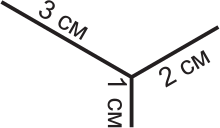
(А) 6 см
(Б) 7 см
(В) 8 см
(Г) 9 см
(Д) 10 см
Задача 7.
Два колёса вращаются одновременно в противоположных направлениях, делая полный оборот за 7 минут. В конце каждой минуты каждая буква внутреннего колёса находится точно перед одной из цифр внешнего колёса. На рисунке показаны начальное положение колёс и положение через минуту. В конце некоторой минуты буква С будет перед цифрой 2. Какая цифра окажется в этот момент перед буквой F?
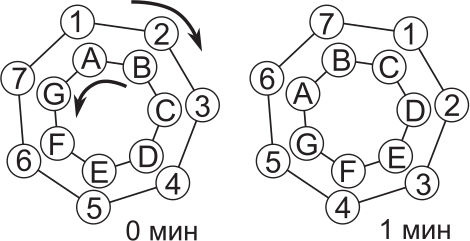
(А) 1
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 8.
В грузовике находится шесть коробок, составленных так, как показано на рисунке. Грузчик выгружает их на землю по одной коробке за раз. При этом он может брать только ту коробку, на которой не стоит никакая другая коробка, и может ставить коробку или на землю, или на другую коробку. Какой из следующих вариантов грузчик не сможет составить?

(А) 
(Б) 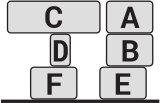
(В) 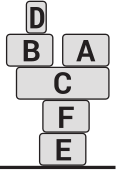
(Г) 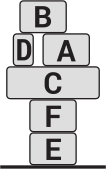
(Д) 
Задача 9.
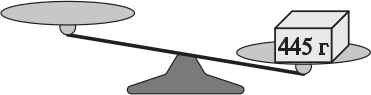
У Пети есть посылка весом 445 г и набор гирь: 
Он кладёт посылку на весы. Какое минимальное количество гирь потребуется, чтобы весы пришли в равновесие?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 10.
Квартиры в доме пронумерованы в порядке возрастания, начиная с 1 (все номера – натуральные числа, ни одно число не пропущено). Кенгуру пересчитал цифры в номерах всех квартир. Он узнал, что цифра 2 встречается 14 раз, а цифра 5 − 3 раза. Какое наибольшее количество квартир может быть в этом доме?
(А) 25
(Б) 26
(В) 34
(Г) 35
(Д) 41
Задача 11.
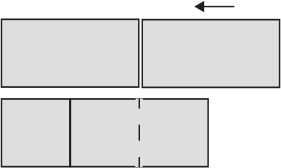
Два одинаковых прямоугольника площадью 18 см2 каждый накладывают друг на друга, как показано на рисунке, и получают в результате новый прямоугольник, который можно разделить на три одинаковых квадрата. Чему равна площадь этого прямоугольника?
(А) 24 см2
(Б) 27 см2
(В) 30 см2
(Г) 32 см2
(Д) 36 см2
Задача 12.
Марине подарили пять коробок (A, B, C, D и E) с разными наборами шоколадных конфет. Конфеты обозначены цифрами от 1 до 9 в соответствии с их вкусами.

Марина съела большую часть конфет, после чего в каждой коробке осталось только по одной конфете. Какая коробка обозначена буквой Х?

(А) A
(Б) B
(В) C
(Г) D
(Д) E
Задача 13.
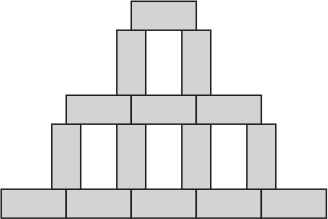
Нина нарисовала конструкцию, состоящую из нескольких одинаковых серых прямоугольников. Ширина конструкции 45 см, высота – 30 см. Чему равна площадь одного серого прямоугольника?
(А) 24 см2
(Б) 27 см2
(В) 30 см2
(Г) 33 см2
(Д) 36 см2
Задача 14.
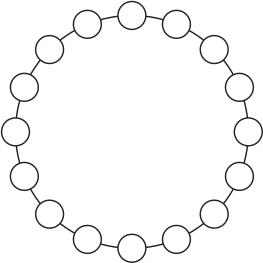
В каждом круге на рисунке написано и скрыто число. Числа в соседних кругах отличаются на единицу. Известно, что в одном из кругов стоит число 5, а в каком-то другом – число 13. Сколько разных чисел записано в этих 16 кругах?
(А) 9
(Б) 10
(В) 13
(Г) 14
(Д) 16
Задача 15.
На рисунке изображены два больших квадрата, площади которых равны. Часть каждого из квадратов закрашена, как показано на рисунке.
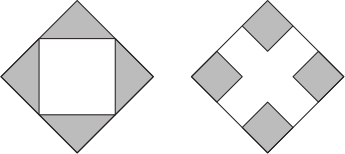
В первом квадрате отрезками соединены середины соседних сторон. Во втором квадрате закрашены четыре квадрата меньшего размера, длины сторон которых равны трети длины стороны большого квадрата. Площадь закрашенной части в первом квадрате равна 9. Чему равна площадь закрашенной части во втором квадрате?
(А) 4
(Б) 8
(В) 9
(Г) 10
(Д) 12
Задача 16.
Перед вами цифры от 0 до 9, написанные шрифтом Брайля для незрячих людей (чёрные точки на рисунке соответствуют выпуклым точкам шрифта Брайля). Сколько различных двузначных чисел, написанных шрифтом Брайля, содержит ровно 5 выпуклых точек?

(А) 16
(Б) 18
(В) 30
(Г) 32
(Д) 34
Задача 17.
На рисунке изображены соты, состоящие из ячеек. В некоторых ячейках есть мёд. Число на каждой ячейке обозначает, в скольких соседних ячейках имеется мёд. Ячейки считаются соседними, если у них есть хотя бы одна общая сторона. Сколько всего ячеек содержат мёд?

(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 11
Задача 18.
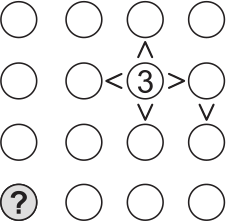
В каждом кружочке Аня записывает по одному целому числу от 1 до 10. Она хочет, чтобы сумма чисел в каждых четырёх кружочках, лежащих на одной прямой линии, была равна 23. Какое число она должна вписать в круг, обозначенный знаком вопроса?
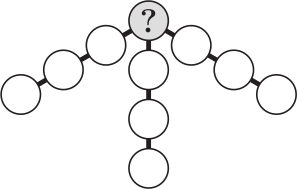
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 19.
У Кристины был белый квадратный лист бумаги. От углов данного квадрата она отрезала четыре квадрата, меньших по размеру, так, как показано на рисунке (1, 2, 3, 6 – длины сторон отрезанных квадратов). После этого площадь оставшейся фигуры составила половину площади исходного квадрата. Чему равен периметр оставшейся фигуры?
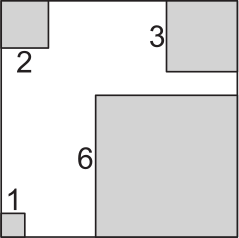
(А) 36
(Б) 40
(В) 44
(Г) 48
(Д) 52
Задача 20.
Рита решает головоломку, расставляя в кружочках числа 1, 2, 3 и 4. В каждой строке и в каждом столбце эти числа должны находиться ровно по одному разу. Кроме того должны выполняться отношения между некоторыми числами, указанные знаками > («больше») и < («меньше»), как в строках, так и в столбцах. Например:
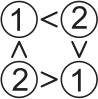
Какое число Рита должна написать в круге, обозначенном знаком вопроса?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) Невозможно определить
Задача 21.
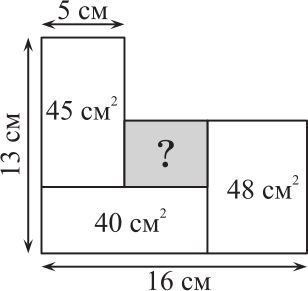
На рисунке изображены четыре прямоугольника. Чему равна площадь прямоугольника, обозначенного знаком вопроса?
(А) 12 см2
(Б) 14 см2
(В) 16 см2
(Г) 18 см2
(Д) 20 см2
Задача 22.
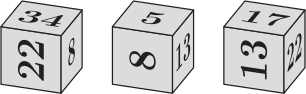
На столе лежат три абсолютно одинаковых кубика. Чему равна сумма чисел на гранях, соприкасающихся со столом?
(А) 26
(Б) 40
(В) 43
(Г) 47
(Д) 56
Задача 23.
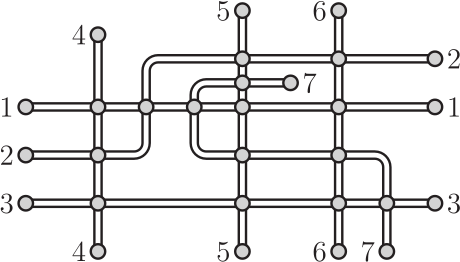
На схеме показаны семь маршрутов поездов. Кружочками обозначены станции. Миша хочет раскрасить эту схему таким образом, чтобы маршруты, имеющие общую станцию, были обозначены разными цветами. Какое наименьшее количество цветов он может использовать?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 24.
Дима складывает кубик из развёртки. Он хочет, чтобы треугольники, имеющие общую сторону на ребре кубика, были окрашены в один цвет. Как ему следует раскрасить белую часть развёртки?
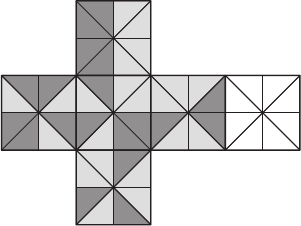
(А) 
(Б) 
(В) 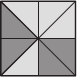
(Г) 
(Д) 
Задача 25.
Семён берёт четыре кружки и случайным образом ставит их на четыре блюдца.

Какое из следующих утверждений верно?
(А) Совершенно точно ни одна кружка не будет стоять на блюдце с таким же рисунком
(Б) Совершенно точно только одна кружка может стоять на блюдце с таким же рисунком
(В) Не может быть такого, чтобы ровно две кружки стояли на блюдцах с такими же рисунками
(Г) Не может быть такого, чтобы ровно три кружки стояли на блюдцах с такими же рисунками
(Д) Не может быть такого, чтобы все четыре кружки стояли на блюдцах с такими же рисунками
Задача 26.
Дан куб, в вершинах которого уже вписано несколько чисел. Лена хочет вписать целые числа от 1 до 5 в оставшиеся вершины так, чтобы сумма чисел в четырёх вершинах каждой грани была одинакова. Какое число она должна поставить в вершину, отмеченную знаком вопроса?
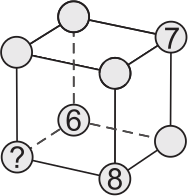
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 27.
У бабушки было некоторое количество конфет. Она решила разделить их поровну между внуками и дала каждому максимально возможное число конфет. В результате оказалось, что внукам досталось по 20 конфет, и 12 конфет остались у бабушки. Какое наименьшее возможное количество конфет было у бабушки изначально?
(А) 52
(Б) 232
(В) 272
(Г) 411
(Д) 432
Задача 28.
Денис хочет разрезать верёвку на 12 равных кусков и отмечает на ней, где он должен сделать разрезы. Максим хочет разрезать эту же верёвку на 16 равных кусков и тоже отмечает на ней, где он должен сделать разрезы. Затем Майя разрезает верёвку во всех местах, которые отметили мальчики. Сколько кусков верёвки получилось у Майи?
(А) 24
(Б) 25
(В) 27
(Г) 28
(Д) 29
Задача 29.
Из деталей пазла Вася хочет составить гусеницу, у которой будет одна голова, один хвост и между ними туловище, состоящее из одной, двух или трёх деталей. Сколько различных гусениц может составить Вася?

(А) 10
(Б) 14
(В) 16
(Г) 18
(Д) 20
Задача 30.
Катя написала на доске трёхзначное число. Затем Лёша дописал к нему ещё одну цифру справа. Он сказал: «Смотри! Твоё число увеличилось на 2024». Какую цифру написал Лёша?
(А) 2
(Б) 3
(В) 4
(Г) 8
(Д) 9

