Задача 12.
Вова хочет сложить квадрат 4 × 4 из четырёх фигур, состоящих из равных квадратиков с числами, так, чтобы сумма чисел во всех строках и столбцах была одинаковая. Никакие фигуры переворачивать нельзя. Три фигуры, которые использует Вова, показаны на рисунке ниже. Какая из следующих фигур должна быть четвёртой?
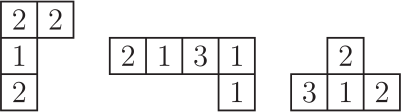
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Ответ на Задачу 12.
Ответ: А
Решение:
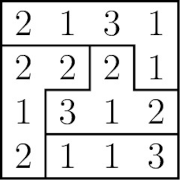
В одной из данных частей есть ряд из четырёх чисел с суммой 2 + 1 + 3 + 1 = 7. Следовательно, сумма чисел во всём квадрате равна 4 ⋅ 7 = 28. Суммы чисел на трёх фигурах равны 7, 8 и 8, и, следовательно, требуется деталь, в которой сумма чисел равна 28 − 7 − 8 − 8 = 5. Из приведённых вариантов единственный с суммой 5 – это A. На рисунке показано, как эти четыре части складываются вместе, образуя квадрат.

