Задача 1.
Какую из пяти резинок нельзя положить так, как показано на рисунке, не разрезая её?
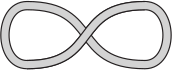
(А) 
(Б) 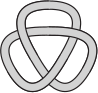
(В) 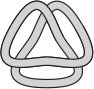
(Г) 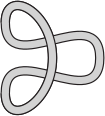
(Д) 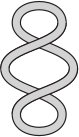
Задача 2.
Фигуру на рисунке складывают из равных между собой пятиугольников. Какой из предложенных ниже пятиугольников нужно поместить в центр образовавшейся фигуры, чтобы получилось изображение двух замкнутых линий?
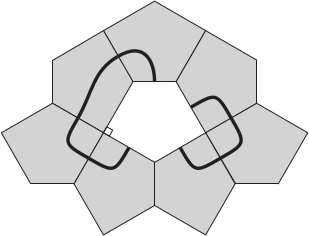
(А) 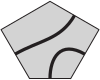
(Б) 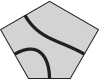
(В) 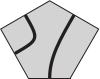
(Г) 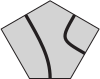
(Д) 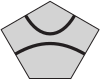
Задача 3.
На рисунке 1 изображён ромб. К нему дорисовали два одинаковых прямоугольных треугольника так, как показано на рисунке 2, и получили пятиугольник. На сколько процентов площадь пятиугольника больше площади ромба?
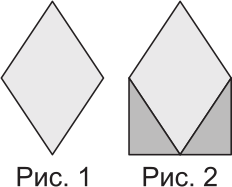
(А) 20%
(Б) 25%
(В) 30%
(Г) 40%
(Д) 50%
Задача 4.
Чему равно значение выражения $\displaystyle \frac{20\times24}{2\times0 + 2\times4}$ ?
(А) 12
(Б) 30
(В) 48
(Г) 60
(Д) 120
Задача 5.
Игорь обрезал все четыре вершины правильного тетраэдра (на рисунке отрезанные части закрашены тёмно-серым). Сколько вершин у получившегося многогранника?
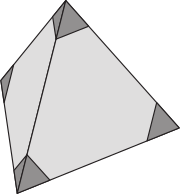
(А) 8
(Б) 9
(В) 11
(Г) 12
(Д) 16
Задача 6.
У Риты есть три жетона с числами 1, 5 и 11:  . Она хочет положить их рядом так, чтобы получилось четырёхзначное число. Сколько различных четырёхзначных чисел она сможет составить?
. Она хочет положить их рядом так, чтобы получилось четырёхзначное число. Сколько различных четырёхзначных чисел она сможет составить?
(А) 3
(Б) 4
(В) 6
(Г) 8
(Д) 9
Задача 7.
На тарелке лежит пять разных фруктов и ягод:  . Алиса любит
. Алиса любит  . Боря любит
. Боря любит  . Коля любит
. Коля любит  . Денис любит
. Денис любит  . Ева любит
. Ева любит  . Каждый из ребят взял с тарелки что-то одно из того, что он любит. При этом все они взяли разные фрукты или ягоды. Кто взял
. Каждый из ребят взял с тарелки что-то одно из того, что он любит. При этом все они взяли разные фрукты или ягоды. Кто взял  ?
?
(А) Алиса
(Б) Боря
(В) Коля
(Г) Денис
(Д) Ева
Задача 8.
Из-за ограничений по весу лифт может перевозить либо 12 взрослых, либо 20 детей. В соответствии с этими ограничениями, какое наибольшее количество детей может поехать в лифте вместе с девятью взрослыми?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 8
Задача 9.
Четыре различных натуральных числа были вписаны в таблицу, а затем скрыты. Произведения чисел в каждом столбце и каждой строке указаны на рисунке. Чему равна сумма всех четырёх чисел в таблице?
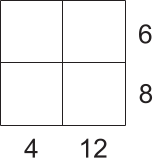
(А) 10
(Б) 12
(В) 13
(Г) 14
(Д) 15
Задача 10.
Длина четырёх тележек из супермаркета, составленных одна в другую, 108 см. Длина десяти тележек из супермаркета, составленных одна в другую, 168 см. Какова длина одной такой тележки?

(А) 60 см
(Б) 68 см
(В) 78 см
(Г) 88 см
(Д) 90 см
Задача 11.
Карина испекла торт и разрезала его на десять равных кусков. Она съела один кусок, а оставшиеся куски расположила на тарелке равномерно, как показано на рисунке. Чему равна градусная мера угла между двумя соседними кусками торта?
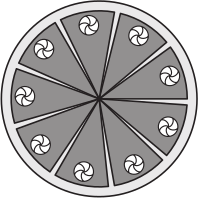
(А) 5°
(Б) 4°
(В) 3°
(Г) 2°
(Д) 1°
Задача 12.
Вова хочет сложить квадрат 4 × 4 из четырёх фигур, состоящих из равных квадратиков с числами, так, чтобы сумма чисел во всех строках и столбцах была одинаковая. Никакие фигуры переворачивать нельзя. Три фигуры, которые использует Вова, показаны на рисунке ниже. Какая из следующих фигур должна быть четвёртой?
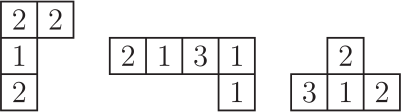
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 13.
Длина стороны квадрата – 10 м. Его поделили на части прямыми линиями, как показано на рисунке. Площади двух закрашенных треугольников равны соответственно А и B. Чему равно значение (А − В)?
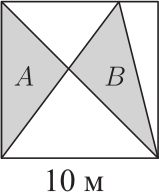
(А) 0 м2
(Б) 1 м2
(В) 2 м2
(Г) 5 м2
(Д) 10 м2
Задача 14.
Пингвин каждый день ходит на рыбалку и приносит 12 рыб для своих двух птенцов. Каждый день он даёт первому увиденному птенцу 7 рыб, а второму – 5 рыб. Пингвинята съедают сразу всех рыб. За последние несколько дней один птенец съел 44 рыбы. Сколько рыб съел за эти дни другой птенец?
(А) 34
(Б) 40
(В) 46
(Г) 52
(Д) 58
Задача 15.
Илья составляет конструкцию: ко всем граням одного кубика он приклеивает такие же кубики. Теперь он хочет к каждой грани этой конструкции также приклеить по кубику. Сколько кубиков ему для этого потребуется?
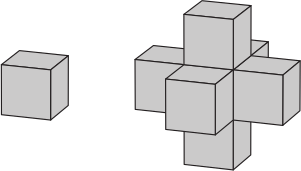
(А) 18
(Б) 16
(В) 14
(Г) 12
(Д) 10
Задача 16.
Кенгуру прыгает вверх в гору, а затем обратно вниз тем же маршрутом. Когда он двигается вниз, за один прыжок он преодолевает в три раза большее расстояние, чем когда он двигается вверх. По дороге в гору длина одного прыжка Кенгуру составляет 1 метр. Всего по дороге в гору и обратно Кенгуру совершил 2024 прыжка. Какой путь он преодолел суммарно в обе стороны?
(А) 506 м
(Б) 1012 м
(В) 2024 м
(Г) 3036 м
(Д) 4048 м
Задача 17.
Большой прямоугольник разрезали на четыре меньших прямоугольника. Периметры трёх из них равны 16, 18 и 24 (смотри рисунок). Чему равен периметр четвёртого прямоугольника?
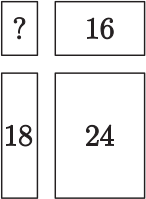
(А) 8
(Б) 10
(В) 12
(Г) 14
(Д) 16
Задача 18.
Вода составляет 80% массы свежих грибов. При этом вода составляет лишь 20% массы сушёных грибов. На сколько процентов уменьшается масса грибов при сушке?
(А) 60%
(Б) 70%
(В) 75%
(Г) 80%
(Д) 85%
Задача 19.
Девять карточек с различными целыми числами от 1 до 9 включительно разложены на столе лицевой стороной вниз. Саша, Миша, Кира и Даша взяли наугад по две карточки каждый.
- Саша сказал: «Сумма моих чисел равна 6».
- Миша сказал: «Разность моих чисел равна 5».
- Кира сказала: «Произведение моих чисел равно 18».
- Даша сказала: «Одно из моих чисел в два раза больше другого».
Все четверо сказали правду. Какое число осталось на столе?
(А) 1
(Б) 3
(В) 6
(Г) 8
(Д) 9
Задача 20.
Правильный пятиугольник и правильный шестиугольник соединены с квадратом, как показано на рисунке. Чему равен угол α?
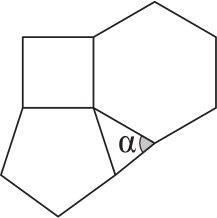
(А) 24°
(Б) 42°
(В) 60°
(Г) 69°
(Д) 74°
Задача 21.
Цифры от 0 до 9 могут быть написаны сочетанием вертикальных и горизонтальных чёрточек. Гена выбрал три различных цифры. Вместе они содержат 5 горизонтальных и 10 вертикальных чёрточек. Чему равна сумма этих трёх цифр?

(А) 9
(Б) 10
(В) 14
(Г) 18
(Д) 19
Задача 22.
Таня хочет закрасить ещё два квадрата на рисунке так, чтобы полученное изображение имело единственную ось симметрии. Сколькими различными способами она может это сделать?

(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 23.
На рисунке изображены три полукруга, расположенные внутри прямоугольника. Средний полукруг касается двух соседних полукругов, а они, в свою очередь, касаются коротких сторон прямоугольника. Самый большой полукруг также касается верхней длинной стороны прямоугольника. Кратчайшие расстояния от этой стороны до двух других полукругов равны 5 см и 7 см. Чему равен периметр прямоугольника?
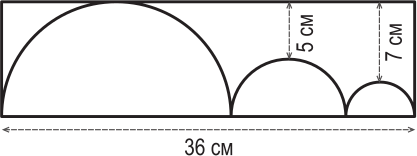
(А) 82 см
(Б) 92 см
(В) 96 см
(Г) 108 см
(Д) 120 см
Задача 24.
Группа из 50 учеников села в круг. Они бросают мяч по кругу. Каждый ученик, получивший мяч, бросает его по направлению против часовой стрелки шестому по счёту от себя ученику, и тот его ловит. Федя получил мяч сто раз. Сколько учеников за это время так и не получили мяч?
(А) 0
(Б) 8
(В) 10
(Г) 25
(Д) 40
Задача 25.
На рисунке изображена пирамида из квадратов, в которые Даня хочет вписать натуральные числа так, чтобы каждый квадрат в средней и верхней строках содержал произведение двух чисел, написанных непосредственно под ним. Если самое верхнее число 720, то сколько различных значений может принимать число n?
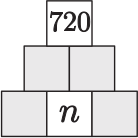
(А) 1
(Б) 4
(В) 5
(Г) 6
(Д) 8
Задача 26.
Фермер продаёт куриные и утиные яйца. Он привёз на рынок шесть корзин, в которых находится 4, 6, 12, 13, 22 и 29 яиц соответственно. Первый покупатель купил одну корзину яиц. После этого фермер заметил, что у него осталось в два раза больше куриных яиц, чем утиных. Сколько яиц купил первый покупатель?
(А) 4
(Б) 12
(В) 13
(Г) 22
(Д) 29
Задача 27.
Три угла построены на клетчатом листе бумаги, как показано на рисунке, и отмечены буквами α, β и γ. Чему равно значение (α + β + γ)?
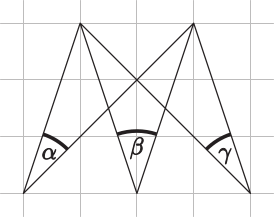
(А) 60°
(Б) 70°
(В) 75°
(Г) 90°
(Д) 120°
Задача 28.
Капитан Флинт попросил четырёх пиратов написать, сколько золотых, серебряных и бронзовых монет было в сундуке с сокровищами. Они написали это на листке. Однако, к несчастью, часть листка оторвалась и потерялась. Известно, что только один из четырёх пиратов написал правду. Остальные трое соврали во всех трёх ответах. Также известно, что всего в сундуке было 30 монет. Кто из пиратов написал правду?
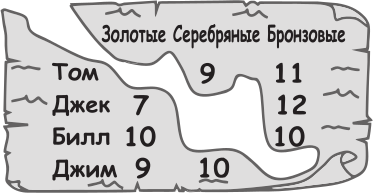
(А) Том
(Б) Джек
(В) Билл
(Г) Джим
(Д) Нельзя определить
Задача 29.
Первый автомобилист поехал из точки А в точку В и сразу же вернулся обратно в точку А. Второй автомобилист поехал из точки B в точку А и сразу же вернулся обратно в точку В. Они ехали по одной и той же дороге, стартовали в одно и то же время, и скорость каждого из них была постоянной на протяжении всего пути. Скорость первого автомобилиста в 3 раза выше скорости второго. В первый раз они встретились через 15 минут после старта. Через какое время после старта они встретились во второй раз?
(А) 20 мин
(Б) 25 мин
(В) 30 мин
(Г) 35 мин
(Д) 45 мин
Задача 30.
На рисунке АВ = 2 см, ВС = 6 см, CD = 8 см, DE = 4 см и ∠ACE = 90°. Чему равна площадь четырёхугольника BCDF?
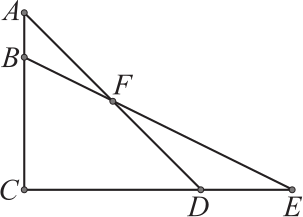
(А) 24 см2
(Б) 28 см2
(В) 32 см2
(Г) 36 см2
(Д) 48 см2

