Задача 23.
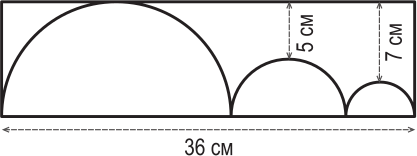
На рисунке изображены три полукруга, расположенные внутри прямоугольника. Средний полукруг касается двух соседних полукругов, а они, в свою очередь, касаются коротких сторон прямоугольника. Самый большой полукруг также касается верхней длинной стороны прямоугольника. Кратчайшие расстояния от этой стороны до двух других полукругов равны 5 см и 7 см. Чему равен периметр прямоугольника?
(А) 82 см
(Б) 92 см
(В) 96 см
(Г) 108 см
(Д) 120 см
Ответ на Задачу 23.
Ответ: Б
Решение:
Пусть h см – длина короткой стороны прямоугольника. Следовательно, радиусы трёх полукругов в см равны h, h − 5 и h − 7. Следовательно, рассматривая длинную сторону прямоугольника, мы имеем 2 ⋅ (h + h − 5 + h − 7) = 36. Решая, получаем h = 10. Следовательно, периметр прямоугольника в см равен 2 ⋅ (36 + 10) = 92.

