Задача 25.
На рисунке изображена пирамида из квадратов, в которые Даня хочет вписать натуральные числа так, чтобы каждый квадрат в средней и верхней строках содержал произведение двух чисел, написанных непосредственно под ним. Если самое верхнее число 720, то сколько различных значений может принимать число n?
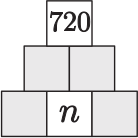
(А) 1
(Б) 4
(В) 5
(Г) 6
(Д) 8
Ответ на Задачу 25.
Ответ: Г
Решение:
Пусть a и b — числа, которые стоят в левой и правой частях нижней строки соответственно. Следовательно, значения в полях среднего ряда — это an и bn, а значение в верхнем ряду — abn2. Однако abn2 = 720. Следовательно, n — квадратичный множитель числа 720. Разложим число на простые множители: 720 = 1 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 5 и, следовательно, n может быть равно 1, 2, 3, 4, 6 или 12. Итого шесть различных значений.

