Задача 28.
Капитан Флинт попросил четырёх пиратов написать, сколько золотых, серебряных и бронзовых монет было в сундуке с сокровищами. Они написали это на листке. Однако, к несчастью, часть листка оторвалась и потерялась. Известно, что только один из четырёх пиратов написал правду. Остальные трое соврали во всех трёх ответах. Также известно, что всего в сундуке было 30 монет. Кто из пиратов написал правду?
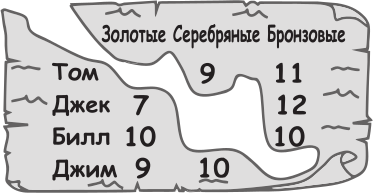
(А) Том
(Б) Джек
(В) Билл
(Г) Джим
(Д) Нельзя определить
Ответ на Задачу 28.
Ответ: Б
Решение:
Предположим, Том сказал правду. Тогда, поскольку общее количество монет равно 30, его ответ для золотых монет будет равен 30 − 9 − 11 = 10. Однако это то же самое, что и ответ Билла для золотых монет. И поскольку три пирата, которые солгали, солгали во всех трёх своих ответах, это предположение невозможно. Теперь предположим, что Билл сказал правду. Его ответ для серебряных монет будет 30 − 10 − 10 = 10, но это то же самое, что и ответ Джима, и потому данное предположение тоже невозможно. Далее предположим, что Джим сказал правду. Его ответ для бронзовых монет будет 30 − 9 − 10 = 11. Но такой же ответ у Тома, а значит и это предположение невозможно. Следовательно, только Джек мог сказать правду. Его пропущенный ответ для серебряных монет будет 30 − 7 − 12 = 11, и видно, что ни один из его ответов не соответствует ни одному ответу других пиратов.

