Задача 30.
На рисунке АВ = 2 см, ВС = 6 см, CD = 8 см, DE = 4 см и ∠ACE = 90°. Чему равна площадь четырёхугольника BCDF?
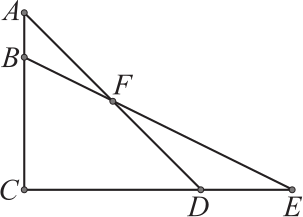
(А) 24 см2
(Б) 28 см2
(В) 32 см2
(Г) 36 см2
(Д) 48 см2
Ответ на Задачу 30.
Ответ: Б
Решение:
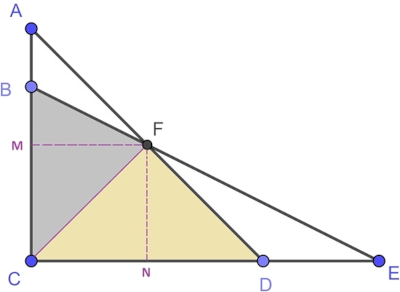
Соединим точки С и F, и построим FM и FN перпендикулярно АС и СЕ соответственно (см. рисунок). Тогда площадь четырёхугольника BCDF будет складываться из площадей треугольников BCF и CFD. Площадь ABF = 1/2∙AB∙FM = 1/2∙2∙FM, площадь BCF = 1/2∙BC∙FM = 1/2∙6∙FM. Тогда Площадь ABF = 1/3 площади BCF. Аналогично Площадь FDE = 1/2∙DE∙FN = 1/2∙4∙FN, площадь CFD = 1/2∙CD∙FN = 1/2∙8∙FN. Тогда Площадь FDE = 1/2 площади CFD. Рассмотрим прямоугольный треугольник АСD. Площадь ACD = 1/2∙AC∙CD = 1/2∙8∙8 = 32. Аналогично площадь прямоугольного треугольника BCE = 1/2∙BC∙CE = 1/2∙6∙12 = 36. В свою очередь площадь ACD = площадь ABF + площадь BCF + площадь CFD = 1/3 площади BCF + площадь BCF + площадь CFD = 4/3 площади BCF + площадь CFD. А площадь ВСЕ = площадь BCF + площадь CFD + площадь FDE = площадь BCF + площадь CFD + 1/2 площади CFD = площадь BCF + 3/2 площади CFD. Обозначим площадь BCF как х, площадь CFD как у. Тогда имеем систему уравнений: 4/3x + y = 32, x + 3/2 = 36. Отсюда х = 12, у = 16. Тогда площадь четырёхугольника BCDF = площадь BCF + площадь CFD = 12 + 16 = 28 кв.см.

