Международный конкурс по математике Кенгуру, 9-11 класс, 2024 год
дата проведения: 21 марта 2024
Задача 11.
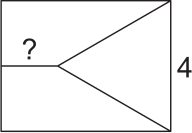
Прямоугольник разделён на три части, одна из которых является равносторонним треугольником со стороной 4, а две другие – трапеции. Площади всех трёх частей равны. Какова длина меньшего основания трапеций?
(А) √2 см
(Б) √3 см
(В) 2√2 см
(Г) 3 см
(Д) 2√3 см
Ответ на Задачу 11.
Ответ: Б
Решение:
Высота треугольника 4∙√3 / 2 = 2√3, а его площадь 1/2 ⋅ 4 ⋅ 2√3 = 4√3. Тогда площадь всего прямоугольника равна 3 ⋅ 4√3 = 12√3. Тогда его длина 12√3 : 4 = 3√3. И тогда искомая нам сторона трапеции равна 3√3 − 2√3 = √3.

