Задача 1.
Чему равно значение выражения $\displaystyle \frac{2 \times 0.24}{20 \times 2.4}$ ?
(А) 0,01
(Б) 0,1
(В) 1
(Г) 10
(Д) 100
Задача 2.
Какой из квадратов поделён на две фигуры, формы которых не одинаковы?
(А) 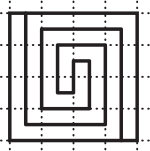
(Б) 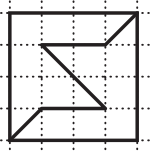
(В) 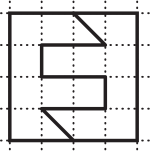
(Г) 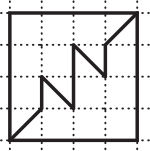
(Д) 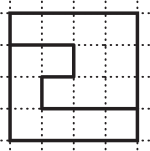
Задача 3.
Суммарное количество точек на каждой паре противоположных граней кубика равно 7. Назовём суммой вершины кубика сумму количества точек на тех гранях, для которых эта вершина будет общей. Вершина Р общая для граней, на которых находятся 1, 2 и 3 точки, то есть сумма вершины Р равна 6 = 1 + 2 + 3. Чему равна наибольшая из сумм вершин Q, R и S ?
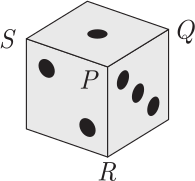
(А) 7
(Б) 9
(В) 10
(Г) 11
(Д) 15
Задача 4.
На рисунке показаны несколько первых движений игры в прыжки. Последовательность изображений повторяется каждые четыре клетки. Игрок должен прыгать, приземляясь на ноги так, как нарисовано в каждой клетке.

Майя прыгнула ровно на 48 клеток, начиная с левой ноги. Сколько раз её левая нога коснулась клеток?
(А) 12
(Б) 24
(В) 36
(Г) 40
(Д) 48
Задача 5.
На рисунке изображена фигура из шести отрезков с указанными длинами.
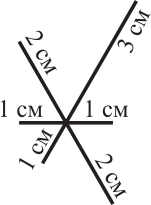
Тимур хочет нарисовать эту фигуру, не отрывая карандаш от бумаги. Начать рисовать можно с любого места. Какова длина наименьшего пути, который Тимур должен провести, чтобы получить желаемый результат?
(А) 14 см
(Б) 15 см
(В) 16 см
(Г) 17 см
(Д) 18 см
Задача 6.
На рисунке изображён квадрат с четырьмя кругами одинаковой площади, каждый из которых касается двух сторон квадрата и двух других кругов. Каково соотношение площадей чёрной и серой областей?
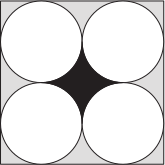
(А) 1 : 4 7
(Б) 1 : 3
(В) 2 : 3
(Г) 3 : 4
(Д) π : 1
Задача 7.
Дима составляет на столе последовательность конструкций, начиная с одного кубика. Новую конструкцию он получает, добавляя пять кубиков – по одному к каждой видимой грани исходного кубика – как показано на рисунке. Какое наименьшее количество кубиков нужно добавить к полученной конструкции, чтобы все её видимые грани оказались скрыты?
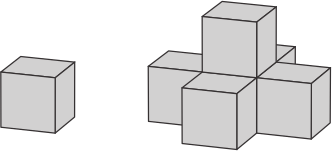
(А) 8
(Б) 9
(В) 10
(Г) 13
(Д) 19
Задача 8.
Трёхзначный палиндром — это число вида «aba», где цифры a и b могут быть как одинаковыми, так и разными. Какова сумма цифр наибольшего трёхзначного палиндрома, который при этом будет кратен 6?
(А) 16
(Б) 18
(В) 20
(Г) 21
(Д) 24
Задача 9.
Миша нарисовал квадрат ABCD. Затем он дорисовал к нему правильный шестиугольник со стороной ОС, где О – центр квадрата. Чему равен угол α?
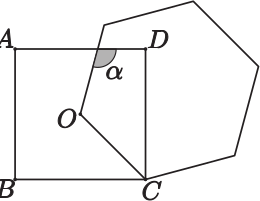
(А) 105°
(Б) 110°
(В) 115°
(Г) 120°
(Д) 125°
Задача 10.
Фермер огораживает прямоугольное поле 40-метровым забором. Длина каждой стороны поля выражается простым числом. Какова максимально возможная площадь поля?
(А) 99 м2
(Б) 96 м2
(В) 91 м2
(Г) 84 м2
(Д) 51 м2
Задача 11.
Прямоугольник разделён на три части, одна из которых является равносторонним треугольником со стороной 4, а две другие – трапеции. Площади всех трёх частей равны. Какова длина меньшего основания трапеций?
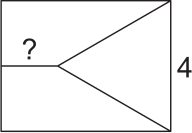
(А) √2 см
(Б) √3 см
(В) 2√2 см
(Г) 3 см
(Д) 2√3 см
Задача 12.
Лена расставляет буквы A, B, C и D в таблице размером 2 × 4.
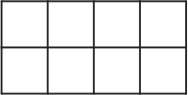
В каждой ячейке может находиться ровно одна буква. Лена хочет, чтобы в каждой строке и в каждом квадрате размером 2 × 2 каждая из четырёх букв встречалась ровно один раз. Сколькими способами она может разместить буквы так, чтобы выполнялось это условие?
(А) 12
(Б) 16
(В) 20
(Г) 24
(Д) 48
Задача 13.
Саша вырезал из картона три круга разных цветов. Он положил их друг на друга, как показано на рисунке 1. Затем он переместил круги так, чтобы все три круга касались друг друга, как показано на рисунке 2.
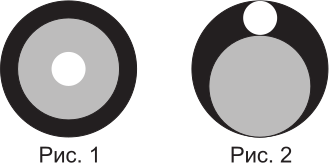
На первом рисунке площадь видимой чёрной области в семь раз больше площади белого круга. Каково соотношение площадей видимой чёрной области на первом и втором рисунках?
(А) 3 : 1
(Б) 4 : 3
(В) 6 : 5
(Г) 7 : 6
(Д) 9 : 7
Задача 14.
Дочь Марии сегодня родила девочку. Через два года произведение возрастов Марии, её дочери и внучки будет равно 2024. При этом сейчас возраст Марии и её дочери — это чётные числа. Сколько сейчас лет Марии?
(А) 42
(Б) 44
(В) 46
(Г) 48
(Д) 50
Задача 15.
Точка P выбрана внутри равностороннего треугольника АВС. Из точки Р проведены три отрезка параллельно сторонам, как показано на рисунке. Длины этих отрезков составляют 2 м, 3 м и 6 м. Каков периметр треугольника АВС?
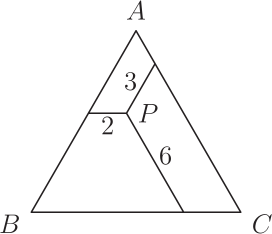
(А) 22 м
(Б) 26 м
(В) 33 м
(Г) 39 м
(Д) 44 м
Задача 16.
В двенадцати кругах на рисунке написаны и затем скрыты некоторые целые положительные числа. Число внутри каждого квадрата – это произведение чисел в его четырёх вершинах. Чему равно произведение чисел в восьми серых кругах?
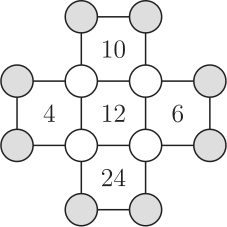
(А) 20
(Б) 40
(В) 80
(Г) 120
(Д) 480
Задача 17.
На столе стоят четыре вазы, в которые разложили несколько конфет. Количество конфет в первой вазе совпадает с количеством ваз, в которых находится одна конфета. Количество конфет во второй вазе совпадает с количеством ваз, в которых находятся две конфеты. Количество конфет в третьей вазе совпадает с количеством ваз, в которых находятся три конфеты. Количество конфет в четвёртой вазе совпадает с количеством ваз, в которых нет конфет. Сколько всего конфет находится в четырёх вазах?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 18.
У Жени есть n3 (где n > 2) одинаковых кубиков. Из всех этих кубиков он сложил большой куб. Затем он покрасил всю внешнюю поверхность этого большого куба. Количество маленьких кубиков с одной закрашенной гранью при этом оказалось равно количеству кубиков без закрашенных граней. Чему равно значение n?
(А) 4
(Б) 6
(В) 7
(Г) 8
(Д) 10
Задача 19.
У Кристины есть набор карточек с номерами от 1 до 12. Она размещает восемь из них в вершинах восьмиугольника так, чтобы сумма каждой пары чисел, находящихся в двух вершинах, соединённых общей стороной восьмиугольника, была кратна 3. Какие числа Кристина не использовала?
(А) 1, 5, 9, 12
(Б) 3, 5, 7, 9
(В) 1, 2, 11, 12
(Г) 5, 6, 7, 8
(Д) 3, 6, 9, 12
Задача 20.
Олег нарисовал некоторое изображение, используя комбинацию квадратов и равносторонних треугольников, как показано на рисунке 1. Длины сторон каждого квадрата и каждого треугольника равны 1 см. Затем он вырезал это изображение и сложил из него трёхмерную фигуру, показанную на рисунке 2. Чему равно расстояние между вершинами А и В?
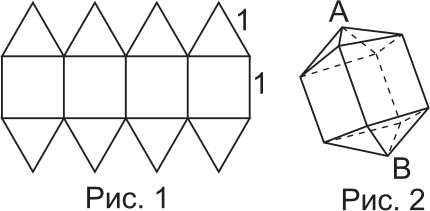
(А) √5 см
(Б) (1 + √2) см
(В) 5 / 2 см
(Г) (1 + √3) см
(Д) 2√2 см
Задача 21.
Число n! (n! = 1 ∙ 2 ∙ … ∙ n) разложили на простые множители: Простые числа в этой записи идут в порядке возрастания. Чернилами закрашены некоторые простые числа и некоторые показатели степеней. Какова степень у числа 17 в этой записи?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 22.
Коля весь день либо говорит только правду, либо только лжёт. В один день он сказал ровно четыре из пяти представленных ниже фраз. Какую фразу он не мог сказать в тот день?
(А) Я лгал вчера и буду лгать завтра
(Б) Я говорю правду сегодня и буду говорить правду завтра
(В) 2024 делится на 11
(Г) Вчера была среда
(Д) Завтра будет суббота
Задача 23.
Сумма цифр целого положительного числа N больше суммы цифр числа N + 1 в три раза. Чему равно наименьшее возможное значение суммы цифр числа N?
(А) 9
(Б) 12
(В) 15
(Г) 18
(Д) 27
Задача 24.
У Даши есть несколько чёрных, серых и белых кубиков. 27 кубиков из этого набора она использует, чтобы построить куб 3 × 3 × 3. Она хочет, чтобы его поверхность была ровно на одну треть чёрной, на одну треть серой и на одну треть белой. Наименьшее возможное количество чёрных кубиков, которое она может использовать, равно A, а максимально возможное количество чёрных кубиков, которое она может использовать, равно B. Чему будет равно значение (B − A)?
(А) 1
(Б) 3
(В) 6
(Г) 7
(Д) 9
Задача 25.
Аня подбросила игральный кубик 24 раза. Все числа от 1 до 6 выпали хотя бы один раз. Число 1 выпало больше раз, чем любое другое число. Аня сложила все выпавшие числа. Сумма, которую она получила, оказалась самой большой из возможных. Каково значение этой суммы?
(А) 83
(Б) 84
(В) 89
(Г) 90
(Д) 100
Задача 26.
Оля гуляла по парку. Половину всего времени она шла со скоростью 2 км/ч. Половину всего расстояния она прошла со скоростью 3 км/ч. Остальное время она шла со скоростью 4 км/ч. Какую часть времени всей прогулки она шла со скоростью 4 км/ч?
(А) $\displaystyle \frac{1}{14}$
(Б) $\displaystyle \frac{1}{12}$
(В) $\displaystyle \frac{1}{7}$
(Г) $\displaystyle \frac{1}{5}$
(Д) $\displaystyle \frac{1}{4}$
Задача 27.
Алиса выписала все целые числа от 1 до 25 включительно. Теперь она хочет стереть некоторые из них, а затем разделить оставшиеся числа на две группы так, чтобы произведения чисел в обеих группах были равны. Какое наименьшее количество чисел может стереть Алиса?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 28.
Двадцать точек расположены на окружности на равном расстоянии друг от друга. Каждая из них соединена хордами с остальными девятнадцатью точками. Сколько из этих хорд длиннее радиуса данной окружности, но короче её диаметра?
(А) 90
(Б) 100
(В) 120
(Г) 140
(Д) 160
Задача 29.
На плоскости имеется n различных прямых, обозначенных ℓ1, …, ℓn. Прямая ℓ1 пересекает ровно 5 других прямых, прямая ℓ2 пересекает ровно 9 других прямых, а прямая ℓ3 пересекает ровно 11 других прямых. Каково наименьшее возможное значение n?
(А) 11
(Б) 12
(В) 13
(Г) 14
(Д) 15
Задача 30.
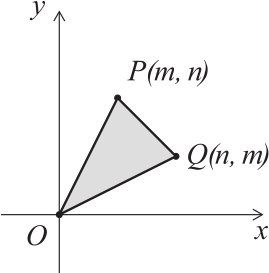
Пусть m и n — целые числа такие, что 0 < m < n. Пусть точки P, Q и O имеют координаты: P(m, n), Q(n, m), и O(0, 0). Для скольких пар (m, n) площадь треугольника OPQ будет равна 2024?
(А) 4
(Б) 6
(В) 8
(Г) 10
(Д) 12

