Задача 12.
Лена расставляет буквы A, B, C и D в таблице размером 2 × 4.
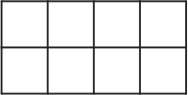
В каждой ячейке может находиться ровно одна буква. Лена хочет, чтобы в каждой строке и в каждом квадрате размером 2 × 2 каждая из четырёх букв встречалась ровно один раз. Сколькими способами она может разместить буквы так, чтобы выполнялось это условие?
(А) 12
(Б) 16
(В) 20
(Г) 24
(Д) 48
Ответ на Задачу 12.
Ответ: Г
Решение:
Буквы A, B, C и D могут свободно располагаться в четырёх квадратах первого ряда. Есть четыре варианта первой буквы, затем три варианта второго квадрата и два варианта третьего квадрата. То есть 4⋅3⋅2⋅1, что равно 24 вариантам. Заполнив первый ряд, рассмотрим второй квадрат второго ряда. Это не может быть буква в первой или третьей позиции первой строки. Значит, это должна быть та же буква, что и в четвёртой позиции. Следовательно, вторая строка однозначно определяется первой строкой, и существует 24 варианта.

