Международный конкурс по математике Кенгуру, 9-11 класс, 2024 год
дата проведения: 21 марта 2024
Задача 16.
В двенадцати кругах на рисунке написаны и затем скрыты некоторые целые положительные числа. Число внутри каждого квадрата – это произведение чисел в его четырёх вершинах. Чему равно произведение чисел в восьми серых кругах?
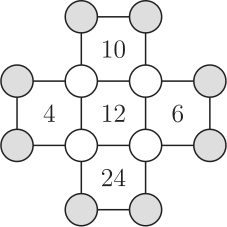
(А) 20
(Б) 40
(В) 80
(Г) 120
(Д) 480
Ответ на Задачу 16.
Ответ: Б
Решение:
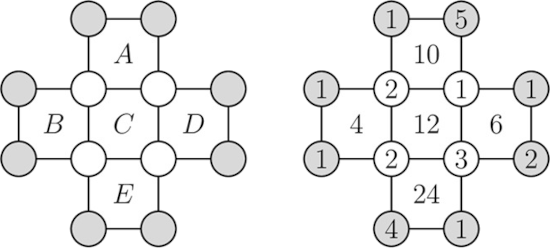
Если внутри квадратов находятся произведения, равные A, B, C, D, E (см. рисунок), то искомое произведение — ABDE / C2. Это связано с тем, что числа в серых кружках включаются в произведения A, B, D и E по одному разу, а числа в белых кружках — дважды. Тогда искомое произведение (4∙10∙6∙24) / 122 = 40. На рисунке справа показан пример возможной конструкции.

