Международный конкурс по математике Кенгуру, 9-11 класс, 2024 год
дата проведения: 21 марта 2024
Задача 19.
У Кристины есть набор карточек с номерами от 1 до 12. Она размещает восемь из них в вершинах восьмиугольника так, чтобы сумма каждой пары чисел, находящихся в двух вершинах, соединённых общей стороной восьмиугольника, была кратна 3. Какие числа Кристина не использовала?
(А) 1, 5, 9, 12
(Б) 3, 5, 7, 9
(В) 1, 2, 11, 12
(Г) 5, 6, 7, 8
(Д) 3, 6, 9, 12
Ответ на Задачу 19.
Ответ: Д
Решение:
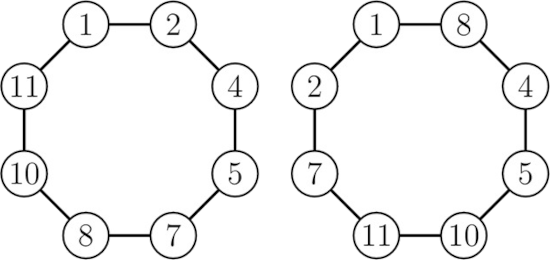
Если одно из чисел в вершине кратно 3, то число в каждой соседней вершине также должно быть кратно 3. Поскольку у нас есть только 4 числа, кратных 3, мы приходим к противоречию. Значит цифры 3, 6, 9, 12 надо убрать. На рисунке приведены два возможных варианта.

