Задача 20.
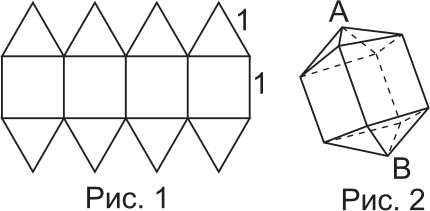
Олег нарисовал некоторое изображение, используя комбинацию квадратов и равносторонних треугольников, как показано на рисунке 1. Длины сторон каждого квадрата и каждого треугольника равны 1 см. Затем он вырезал это изображение и сложил из него трёхмерную фигуру, показанную на рисунке 2. Чему равно расстояние между вершинами А и В?
(А) √5 см
(Б) (1 + √2) см
(В) 5 / 2 см
(Г) (1 + √3) см
(Д) 2√2 см
Ответ на Задачу 20.
Ответ: Б
Решение:
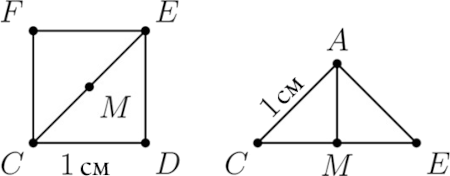
Рассмотрим четырёхугольную пирамиду с вершиной А. Её основанием будет квадрат (назовём его CDEF) со стороной 1 см (см. рисунок). Следовательно, по теореме Пифагора его диагональ CE равна √2 см. Пусть M — середина CE. Тогда AMC — прямоугольный треугольник, гипотенуза AC которого равна 1 см, а катет CM √2/2 см. Опять же, используя теорему Пифагора, получаем: |AM|2 = 1 − (√2/2)2 = 1 − 2/4 = 1/2. Отсюда АМ = 1/√2 = √2/2. Тогда расстояние от А до В будет равно √2/2 + 1 + √2/2 = 1 + √2.

