Задача 24.
У Даши есть несколько чёрных, серых и белых кубиков. 27 кубиков из этого набора она использует, чтобы построить куб 3 × 3 × 3. Она хочет, чтобы его поверхность была ровно на одну треть чёрной, на одну треть серой и на одну треть белой. Наименьшее возможное количество чёрных кубиков, которое она может использовать, равно A, а максимально возможное количество чёрных кубиков, которое она может использовать, равно B. Чему будет равно значение (B − A)?
(А) 1
(Б) 3
(В) 6
(Г) 7
(Д) 9
Ответ на Задачу 24.
Ответ: Г
Решение:
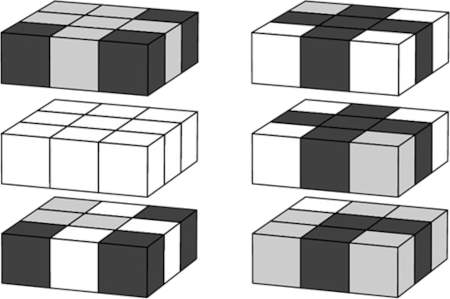
Площадь поверхности куба равна 6 ⋅ 32 = 54. Это означает, что площадь чёрного, серого и белого цвета должна быть равна 54 : 3 = 18 каждая. Каждый маленький кубик куб может давать 3 грани, если это угловой куб, 2 грани, если он находится на ребре, или 1 грань, если он находится в центре грани большого куба. В кубе 3 × 3 × 3 всего 8 угловых кубиков, 12 рёберных кубиков и 6 центров граней. И один кубик расположен полностью внутри большого куба. Наименьшее количество кубиков, составляющих площадь 18, будет в том случае, если использовать только угловые кубики. Тогда А = 6. Наибольшее количество кубиков, составляющих площадь 18, будет, если использовать 6 кубиков, находящихся в центрах граней, и (18 − 6) : 2 = 6 кубиков, находящихся на рёбрах. Кроме того, мы можем взять чёрный кубик в качестве «скрытого» центрального кубика. Тогда В = 6 + 6 + 1 = 13. И тогда B − A = 13 − 6 = 7. Для наглядности см. рисунок.

