Задача 28.
Двадцать точек расположены на окружности на равном расстоянии друг от друга. Каждая из них соединена хордами с остальными девятнадцатью точками. Сколько из этих хорд длиннее радиуса данной окружности, но короче её диаметра?
(А) 90
(Б) 100
(В) 120
(Г) 140
(Д) 160
Ответ на Задачу 28.
Ответ: В
Решение:
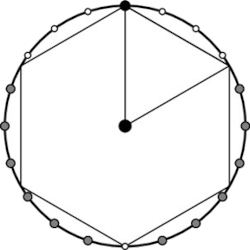
Каждая из 20 точек соединена с 19 другими точками окружности, образуя 19 хорд. Одна из этих 19 хорд точно равна диаметру, поэтому остаётся рассмотреть 18 хорд. Чтобы хорда была больше радиуса, её центральный угол должен быть больше 60 градусов. Поскольку 20 точек образуют правильный 20-угольник, центральный угол хорды, соединяющей две соседние точки, равен 360/20 = 18 градусов. Следовательно, нам нужно как минимум 4 центральных угла (3⋅18 = 54 градуса < 60 градусов). То есть 3 пары хорд от точки до трёх ближайших к ней точек по окружности (с каждой стороны) будут короче радиуса. В результате у нас остаётся 6 пар хорд, или по 12 хорд на точку. Поскольку каждая хорда учитывается дважды (по одному разу для каждой конечной точки), общее количество хорд, удовлетворяющих условию, составляет (20⋅12):2 = 120. Для наглядности см. рисунок.

