Задача 29.
На плоскости имеется n различных прямых, обозначенных ℓ1, …, ℓn. Прямая ℓ1 пересекает ровно 5 других прямых, прямая ℓ2 пересекает ровно 9 других прямых, а прямая ℓ3 пересекает ровно 11 других прямых. Каково наименьшее возможное значение n?
(А) 11
(Б) 12
(В) 13
(Г) 14
(Д) 15
Ответ на Задачу 29.
Ответ: Б
Решение:
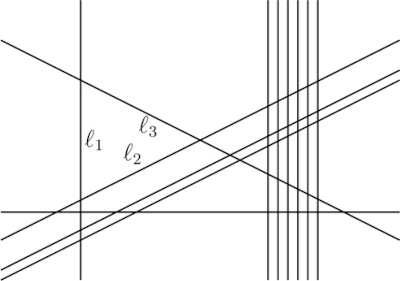
Поскольку одна из прямых пересекает 11 других прямых, минимальное количество прямых равно 12. С другой стороны, взяв семейство из 7 параллельных прямых, другое семейство из 3 параллельных прямых, перпендикулярных первому семейству, и две другие прямые, пересекающие друг друга и пересекая оба семейства параллельных прямых, мы имеем расположение прямых, соответствующее требованию (см. рисунок). Любая из прямых в первом семействе из 7 параллельных прямых может быть ℓ1, поскольку она пересекает 5 других прямых. Любая из прямых во втором семействе из 3 параллельных прямых может быть ℓ2, поскольку она пересекает 9 других прямых. Наконец, любая из последних двух линий может быть ℓ3, поскольку она пересекает 11 других линий. Следовательно, ответ 12.

