Международный конкурс по математике Кенгуру, 9-11 класс, 2024 год
дата проведения: 21 марта 2024
Задача 30.
Пусть m и n — целые числа такие, что 0 < m < n. Пусть точки P, Q и O имеют координаты: P(m, n), Q(n, m), и O(0, 0). Для скольких пар (m, n) площадь треугольника OPQ будет равна 2024?
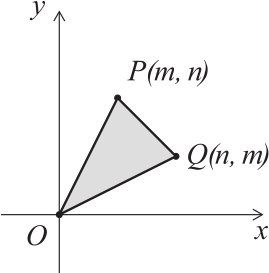
(А) 4
(Б) 6
(В) 8
(Г) 10
(Д) 12
Ответ на Задачу 30.
Ответ: Б
Решение:
S△OPQ = n2 − mn − 1/2(n − m)2 = 1/2(n2 − m2) = 2024. Следовательно (n + m)(n − m) = 4048. Т.к. m и n — целые числа, то n + m и n − m или оба чётные или оба нечётные. Имеется шесть возможностей, чтобы число 4048 = 24⋅11⋅23 было представлено произведением двух чётных чисел: 2⋅2024, 22⋅1012, 23⋅506, (2⋅11)⋅(23⋅23), (22⋅11)⋅(22⋅23), (2⋅23)⋅(23⋅11). Таким образом мы получаем шесть возможных пар (n, m): {(1013, 1011), (508, 504), (257, 249), (103, 81), (68, 24), (67, 21)}.

