Осенний математический Турнир Мёбиуса, 5 класс, 2018 год, первая лига, 4 тур
дата проведения: 31 октября 2018
Задача 6.
На доске записано умножение двух двузначных чисел. Ученик заменил каждую цифру новой, большей предыдущей на одно и то же число. Вот что получилось (см. пример). Какие числа были записаны первоначально?
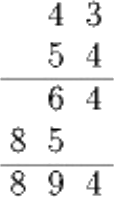
Ответ на Задачу 6.
Пусть разница между цифрами равна 𝑥. Посмотрим на цифру десятков первого слагаемого (𝑎) и цифру единиц второго слагаемого (𝑏): 𝑎 + 𝑥 = 6, 𝑏 + 𝑥 = 5. А их сумма равна 𝑎 + 𝑏 + 𝑥 = 9 или 𝑎 + 𝑏 + 𝑥 = 19 (переход через десяток). В первом случае 𝑥 = 2, во втором 𝑥 = −8 — чего не может быть. Значит, были записаны числа 21 и 32.

