Задача 2.
Можно ли расставить натуральные числа от 1 до 8 в кружки фигуры так, чтобы сумма чисел расположенных на каждой из пяти окружностей была одной и той же?
Ответ на Задачу 2.
Сумма натуральных чисел от 1 до 8 равна 36. Пусть сумма чисел в кружках каждой из пяти окружностей 𝑆.
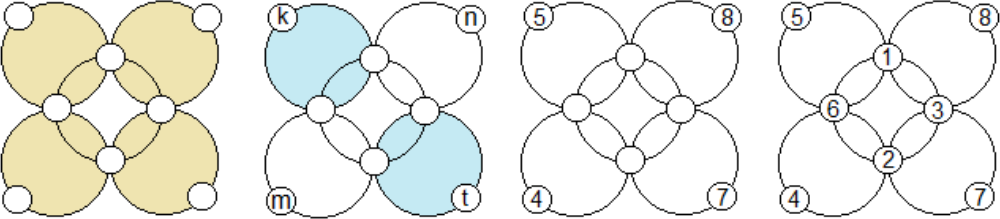
Заметим на рисунке слева, что если найти сумму чисел, расположенных в четырёх закрашенных жёлтым окружностях, то дважды будут посчитаны только числа центральной окружности, поэтому справедливо уравнение 4𝑆 − 𝑆 = 36, поэтому 𝑆 = 12. Далее, на рисунке рядом заметим, что на двух синих окружностях расположены шесть чисел из восьми, то сумма чисел 𝑚 и 𝑛 равна 12, но тогда и сумма чисел 𝑘 и 𝑡 тоже равна 12. В нашем наборе как раз имеются две пары чисел суммой 12 — это 4 и 8, 5 и 7. Расставив эти числа, уже нетрудно расставить остальные.

