Задача 1.
Журнал сшит из двойных листов. Сумма номеров четырёх страниц двойного журнального листа 130. Сколько страниц в этом журнале?
Задача 2.
Можно ли расставить натуральные числа от 1 до 8 в кружки фигуры так, чтобы сумма чисел расположенных на каждой из пяти окружностей была одной и той же?
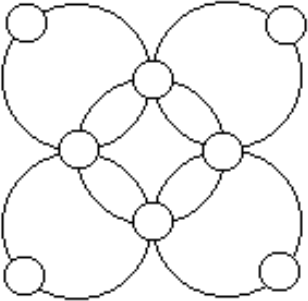
Задача 3.
Решите ребус: ТУРНИР + ОСТРОВ = МИНИБОИ (Одинаковым буквам соответствуют одинаковые цифры, разным — разные.)
Задача 4.
Из шахматной доски вырезали квадратик 2 × 2. Докажите, что оставшуюся часть доски всегда можно разбить на доминошки. (Доминошка — фигура, состоящая из двух соседних по стороне клеток.)
Задача 5.
Говорят, что если подойти к Мёбиусу 2 ноября, то он будет раздавать ленты. Первому подошедшему он даст одну ленту и десятую часть всех оставшихся, второму подошедшему даст две ленты и десятую часть оставшихся, . . . , девятому подошедшему даст девять лент и десятую часть оставшихся. Если же кто-то подойдёт потом, то ему ничего не достанется. Сколько лент есть у Мёбиуса?
Задача 6.
Арсений выписал в ряд натуральные числа от 1 до 2019, затем Костя некоторым образом их переставил, пронумеровал и подписал под каждым номер, а затем Женя для каждой пары чисел (число и его номер) вычел из большего числа меньшее. Могли ли все получившиеся разности оказаться нечётными числами?
Задача 7.
В столовой лежат кусочки сыра и хлеба. Если добавить ещё 20 кусков сыра, то их станет вдвое больше, чем хлеба. Сколько кусков хлеба необходимо убрать, чтобы их стало вдвое меньше, чем сыра?
Задача 8.
Сможет ли Незнайка разрезать квадрат на три шестиугольника, два из которых равны друг другу? (Размеры квадрата могут быть любыми, резать можно не только по линиям сетки.)

