Задача 6.
Игорь выставляет на шахматную доску коней так, чтобы они не били друг друга. У него нашлись только 31 фигурка. Сколькими способами он сможет их все выставить на доску, чтобы желаемое условие выполнялось?
Ответ на Задачу 6.
Разобьём доску на 32 пары клеток ходом коня (конеходы), для этого разобьём поле на прямоугольники 2 × 4, каждый из которых разбивается на конеходы. В каждом конеходе может стоять максимум 1 конь, значит, ровно 1 конеход будет пустым. Тогда при разбиении доски на 4 квадрата 4 × 4 получим, что ровно 3 из них будут содержать по 8 коней, а один квадрат содержит 7 коней. Посмотрим, как можно в квадрате 4 × 4 расставить 8 коней.
Далее на всех рисунках, если не указано иное: к, к1, к2, к3 — конь, х — клетка под боем коня, х1 — клетки, которые окажутся битыми, если в клетку 1 поставить коня, 0 — клетка, в которой не может стоять конь, a-a, б-б и т. д. — конеходы.
В случаях 1.1 − 1.3 пара коней стоит в углу, из них получаются 2 расстановки: «уголки» и «ряды». Если в каждом углу может стоять только 1 конь, не пара (случай 1.4), то в клетках 1-1 и 2-2 не более 1 коня, то получаем расстановку, где все кони стоят на клетках одного цвета. Если в углах нет коней (случай 1.5), то остальные клетки можно разбить на 6 конеходов — максимум 6 коней.
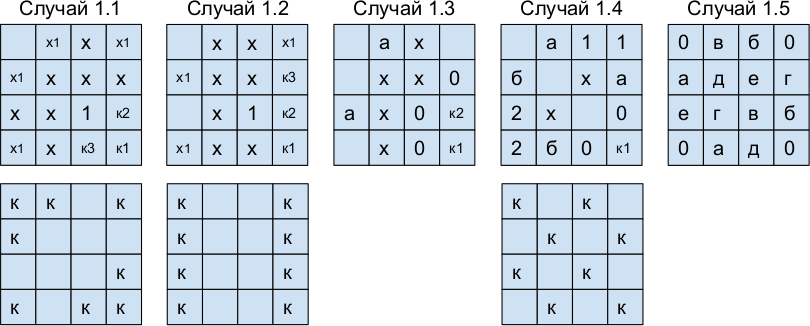
Если в каком-то квадрате 4 × 4 кони расставлены «уголками» (случай 2.1) или «рядами»(случай 2.2), то в соседний квадрат можно поставить не более 6 коней (в 2 × 4 можно поставить не более 4 коней.)
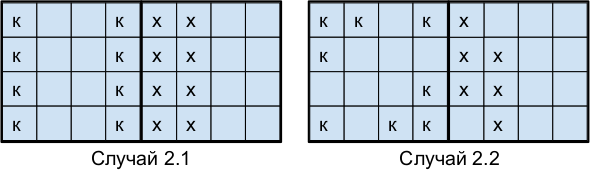
Начав в любом квадрате с 8 конями рассматривать расстановку, мы придём к тому, что в каждом из них кони стоят на одном цвете, при этом в соседних квадратах кони также должны оказаться на одном цвете.
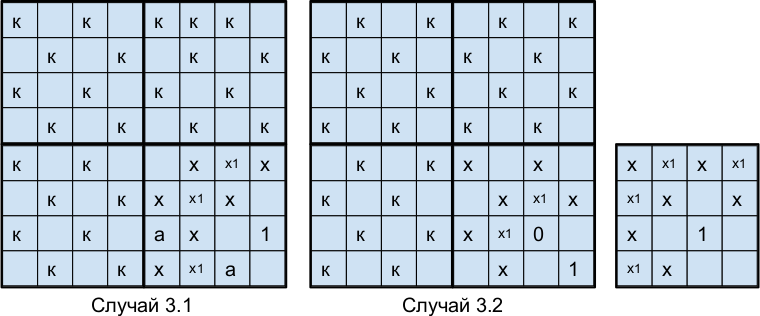
В результате имеем 2 варианта расстановки коней в этих квадратах. Разбор расстановки в 4-м квадрате показывает, что в случае 3.1 остальные 7 коней стоят на том же цвете (если хотя бы один на другом, например 1, то поместится не более 6 коней), а в случае 3.2, кроме расстановки 7 коней на том же цвете ещё возможна расстановка, когда один конь попал на клетку другого цвета и при этом находится в углу (в клетке 0 конь не может стоять, см. рисунок слева) — других расстановок нет. В результате существуют 64 расстановки, когда все кони стоят на одном цвете и одна клетка этого цвета пуста, а также ещё 4 расстановки, когда 30 коней стоят на одном цвете, а ещё один конь на другом цвете в углу доски. Ответ: 68.
Комментарий: Собственно, мы доказали, что на доске 8 × 8 можно расставить 32 коней, не бьющих друг друга, лишь одним способом (с точностью до поворота).

