Задача 5.
В каждой клетке доски 5 × 6 стоит лжец или рыцарь. Лжецы всегда лгут, рыцари всегда говорят правду. Каждый из стоящих на доске сказал: «Среди моих соседей — ровно один рыцарь» (соседями считаются те, кто стоит на клетках, имеющих общую сторону). Сколько рыцарей может быть на доске? (Перечислите все возможности.)
Ответ на Задачу 5.
Если есть хотя бы 1 рыцарь, то найдётся второй (его сосед) — все рыцари разобьются на пары. На рисунках ниже изображены все возможные расстановки пар рыцарей (р1–р1, р2–р2, . . . ) и лжецов (л1, л2, . . . ; а также серые и тёмно-серые клетки), начиная с угловой клетки (номера соответствуют порядку заполнения). Красным выделены клетки, в которых стоят лжецы, имеющие ровно одного соседа рыцаря, либо те, где не могут стоять рыцари, а должны (1, 2, 3). Рассмотрев случаи 1 − 3, получаем, что если в одном из углов стоит лжец, то на доске не должно быть ни одного рыцаря (на доске все лжецы, т. е. 0 рыцарей). В случаях 4.1 − 4.3 рассматриваются все возможные расположения пар рыцарей в углах, и из этого следует единственная расстановка — случай 4.3 (16 рыцарей). Ответ: 0 и 16 рыцарей.
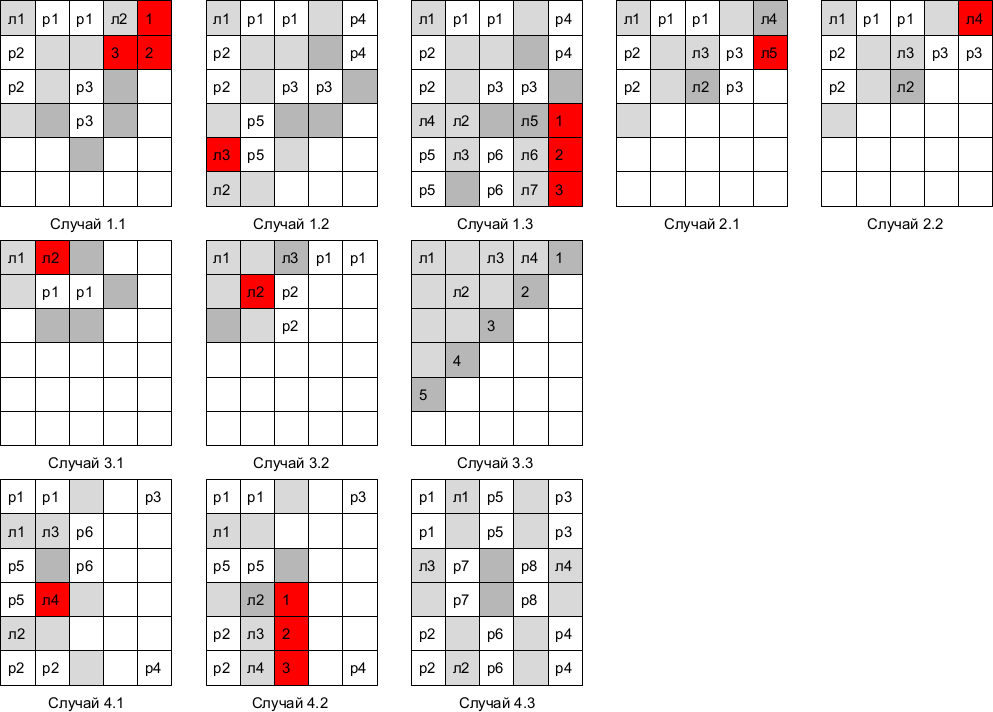
Замечание: Можно доказать, что число рыцарей не превосходит 16, разбив прямоугольник на 2 части 1 × 3 (вместе образуют 1 × 6) и 6 квадратиков 2 × 2. В каждой из 8 частей не может стоять больше 2 рыцарей, откуда рыцарей ≤ 8 · 2 = 16.

