Задача 7.
Шелдон поехал на конференцию, разумеется, на поезде. На весь путь он потратил 𝑡 минут (меньше часа). Ещё он заметил, что на станциях отправления и прибытия угол между часовой и минутной стрелками равнялся 𝑡 градусам. Найдите время, которое Шелдон был в пути.
Ответ на Задачу 7.
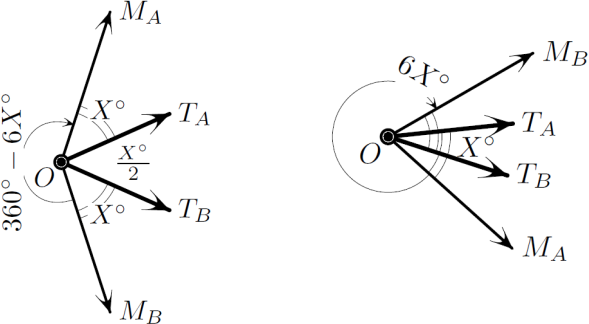
Поскольку между двумя последовательными обгонами часовой стрелки минутной проходит более часа, то за указанное время движения поезда произошло не более одного обгона. Обозначим 𝑂 — центр циферблата, 𝑇𝐴 и 𝑇𝐵 — точки, в которых находился конец часовой стрелки в моменты прохождения поездом начальной станции 𝐴 и конечной 𝐵 соответственно, а 𝑀𝐴 и 𝑀𝐵 — точки, где в эти моменты находился конец минутной стрелки. Заметим также, что за 𝑡 минут часовая стрелка повернулась на 𝑡/2 градусов, а минутная — на 6𝑡 градусов. Тогда, если минутная стрелка обогнала часовую, то точки 𝑇𝐴, 𝑇𝐵, 𝑀𝐴 и 𝑀𝐵 располагаются друг относительно друга так, как левом рисунке. При этом должно выполняться равенство 6𝑡 = 𝑡 + 𝑡 + 𝑡/2, откуда 𝑡 = 0, что противоречит условию задачи. Если же обгона не было, то 𝑇𝐴, 𝑇𝐵, 𝑀𝐴 и 𝑀𝐵 располагаются так, как на правом рисунке, и должно выполняться равенство 360 − 6𝑡 = 𝑡 + 𝑡 − 𝑡/2, откуда 𝑡 = 48.