Осенний математический Турнир Мёбиуса, 6 класс, 2018 год, первая лига, 1 тур
дата проведения: 28 октября 2018
источник: https://moebiustour.ru/archive/tour2
Задача 7.
Из листа бумаги вырезали многоугольник (возможно, треугольник), имеющий ось симметрии. После того, как его сложили по оси симметрии, вновь образовался многоугольник (возможно, треугольник), имеющий ось симметрии. После того, как и его сложили по оси симметрии, образовался треугольник. Сколько сторон могло быть у исходного многоугольника?
Ответ на Задачу 7.
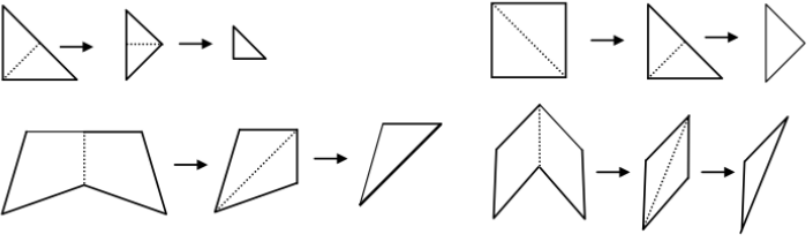
Легко видеть, что 𝑛-угольник может быть получен только из не более чем 2𝑛−2 угольника, так как при разгибании удваивается не более чем 𝑛 − 1 сторона. А значит треугольника мог быть получен только из 3 или 4-угольника, которые, в свою очередь, могли быть получены из 3, 4, 5 или 6-угольника. Примеры приведены на картинке.
