Клара посчитала сумму цифр, с помощью которых записывается сегодняшняя дата: 28.10.2018. Сколько в этом году дат с такой же суммой цифр?

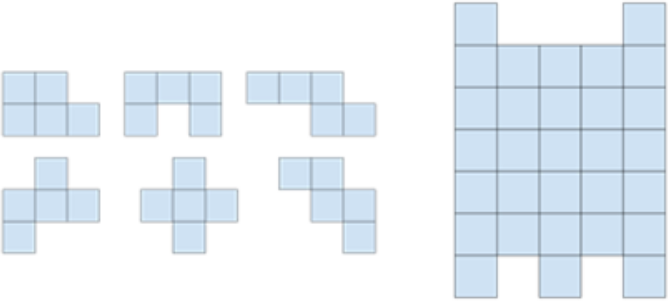
У Андрея есть 6 разных плиток, показанных на рисунке. Сможет ли он собрать узор как на рисунке справа? Нужно использовать все плитки. Все плитки можно поворачивать и переворачивать.

В настольной игре у героев есть 3 способности: сила, ум, отвага. Каждый игрок может выбрать для своего героя одну или две способности. Играют 32 игрока. Известно, что отважных героев (т. е. всех, имеющих способность отвага) в два раза больше умных и в 𝑘 раз меньше, чем сильных (𝑘 — целое число, большее двух). Сколько игроков выбрали одну способность для героя, если известно, что игроков, выбравших 2 способности, на 2 больше, чем отважных?

Кирилл написал на доске всевозможные 9-значные числа, в записи которых встречаются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 по одному разу. Мефодий выбрал из них самое большое и самое маленькое и стёр их. Потом он выбрал самое большое и самое маленькое из оставшихся чисел и тоже их стёр. Мефодий повторял свои действия до тех пор, пока на доске не осталось два числа. Какие это числа?

В строчку выписаны 2018 чисел, каждое из которых больше предыдущего на одну и ту же величину. Может ли среди выписанных чисел быть ровно 102 целых?

Имеется 200 конфет: по 100 ирисок и карамелек. По кругу сидят 100 школьников. Каждому из них раздали 2 ириски или 2 карамельки. Каждую минуту каждый школьник передаёт соседу слева одну ириску, если она у него есть. Если ириски нет, то школьник передаёт карамельку. Докажите, что через несколько минут у всех школьников будет по одно ириске и одной карамельке.

Из листа бумаги вырезали многоугольник (возможно, треугольник), имеющий ось симметрии. После того, как его сложили по оси симметрии, вновь образовался многоугольник (возможно, треугольник), имеющий ось симметрии. После того, как и его сложили по оси симметрии, образовался треугольник. Сколько сторон могло быть у исходного многоугольника?

Натуральное число 𝑛 назовём небольшим, если в его десятичной записи встречаются только цифры 0, 1 или 2. При каком наименьшем 𝑘 любое натуральное число можно представить в виде суммы не более 𝑘 небольших чисел?