Весенний математический Турнир Мёбиуса, 5 класс, 2018 год, первая лига, 2 тур
дата проведения: 18 февраля 2018
Задача 2.
Сколько существует разных квадратов площадью меньше 100 клеточек, которые можно составить из фигурок T-тетрамино?
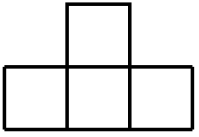
Ответ на Задачу 2.
Фигурки Т-тетрамино состоят из 4 клеток, соответственно количество клеток в квадратах должно делиться на 4. Значит длина стороны должна делится на 2. Квадрат 4 × 4 легко замостить. Значит, можно замостить квадрат 8 × 8 (он состоит из 4 квадратов 4 × 4).
Рассмотрим квадрат 6 × 6. Так как все клетки должны быть замощены Т-тетрамино, значит в каком-то из углов должна стоять Т-тетрамино. Тогда не получится замостить сторону квадрата, 3 клетки которой заняты угловой T-тетрамино (так же можно использовать шахматную раскраску). Можно замостить только квадраты 4 × 4 и 8 × 8.

