Весенний математический Турнир Мёбиуса, 5 класс, 2019 год, первая лига, 1 тур
дата проведения: 18 февраля 2019
Задача 8.
Цифры от 5 до 9 зашифровали буквами, и вышло неравенство:
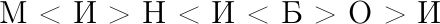
(одинаковыми буквами зашифрованы одинаковые цифры, разными буквами — разные цифры). Чему равна сумма Б + О + М + Б + О + Н?
Ответ на Задачу 8.
Из неравенства следует, что Н и М меньше, чем И, но неизвестно, какая из букв обозначает меньшее число. Ещё известно, что Б > О > И. Следовательно, (Н, М) < И < О < Б. Всего 5 различных букв, и было 5 различных цифр, значит, в неравенстве присутствуют все числа от 5 до 9. Поэтому можно сделать вывод, что зашифровано (5, 6) < 7 < 8 < 9. Тогда сумма равна 2 · 9 + 2 · 8 + 5 + 6 = 45.

