В десятичной записи числа 𝐴 встречаются только цифры 1, 2, 3, 4 (одна и та же цифра в числе может встречаться несколько раз). Каждую цифру числа 𝐴 удвоили и получили число 𝐵. Докажите, что среди чисел 𝐴𝐵 (число 𝐵 приписали справа к числу 𝐴) и 𝐵𝐴 (число 𝐴 приписали справа к числу 𝐵) хотя бы одно не является квадратом натурального числа.

Каждое утро Катерина выпивает чашечку кофе по одной и той же цене в одной и той же кофейне. Чашечка кофе стоит целое число рублей. Известно, что 1000 рублей хватает на 27 чашечек, а 1400 не хватает на 38 чашечек. Сколько может стоить чашечка кофе?

Как на плоскости отметить 11 точек и 10 прямых так, чтобы на 5 проведённых прямых лежало ровно по 3 отмеченные точки, а на других 5 проведённых прямых лежало ровно по 4 отмеченные точки?

Косте подарили двое часов со стрелочками. Но у них есть дефект: одни часы спешат на 15 минут в час, а другие отстают на 5 минут в час. 18 февраля в полдень Костя поставил часы по Московскому времени. Когда часы впервые покажут одно и то же время?

На доске написано записано число. Каждую секунду происходит следующее: сначала последнюю цифру числа на доске стирают, затем к оставшемуся числу прибавляют удвоенную стертую цифру и полученную сумму записывают на доску, полностью стирая старое число. Например, если на доске в какой-то момент появилось число 123, то после него на доске появится число 12 + 3 ⋅ 2 = 18; а если было число 20, то вместо него на доске появится число 2 + 0 ⋅ 2 = 2. Какое число будет на доске через час, если сначала записать на доску число 1102?

На столе лежит набор красных и зелёных кубиков. Костя разложил их все на две кучки так, что в одной из них красных кубиков в два раза больше, чем зелёных, а в другой зелёных в два раза больше, чем красных. Никита разложил все эти же кубики на две кучки так, что в одной красных кубиков в три раза больше, чем зелёных, а в другой зелёных в три раза больше, чем красных. Какое наименьшее количество кубиков могло быть в таком наборе?

Пете подарили набор из 6 гирек, на которых были написаны массы 1 г, 2 г, 3 г, 4 г, 5 г, 6 г; все массы встречались ровно 1 раз. Оказалось, что веса 5 гирек из набора соответствуют надписям на них, а одна гирька оказалась бракованной — её вес меньше указанного. За какое наименьшее количество взвешиваний на чашечных весах без стрелок можно гарантировано найти бракованную гирьку?

Цифры от 5 до 9 зашифровали буквами, и вышло неравенство:

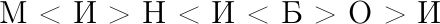
(одинаковыми буквами зашифрованы одинаковые цифры, разными буквами — разные цифры). Чему равна сумма Б + О + М + Б + О + Н?