Замените звёздочки в записи 20 * 20 * 20 * 20 * 20 * 20 * 20 = 2020 на знаки арифметических операций так, чтобы равенство стало верным. Если нужно, можно использовать скобки.

Можно ли разрезать прямоугольник 2019 × 2020 клеток на трёхклеточные уголки?

Перед бароном Мюнхгаузеном на столе лежат три стопки одинаковых по виду монет из 20, 30 и 40 монет. В одной из них есть фальшивая монета другого веса, внешне не отличающаяся от остальных. За какое наименьшее число взвешиваний на чашечных весах без гирь барон сможет найти стопку, в которой все монеты настоящие?

В ряд стоят 10 жителей острова Рыцарей и Лжецов. Пятеро из них сказали: «Справа от меня в ряду есть рыцарь», а пятеро других сказали: «Слева от меня в ряду есть лжец». Какое наибольшее количество лжецов может быть среди них? (Жителями острова Рыцарей и Лжецов являются рыцари, которые всегда говорят правду, и лжецы, которые всегда врут)

Найдите 2020-е по счёту натуральное число, которое нельзя представить в виде произведения двух последовательных натуральных чисел.

На вступительной олимпиаде команды решили в среднем 4 задачи, при этом команды 4 класса решили в среднем 3,6 задачи, а команды 5 класса — 4,2 задачи. Сколько всего было команд, если их меньше 30?

В квадрате 3 × 3 расставлены различные числа от 1 до 9. Назовем парой два числа, стоящие в одной строке или одном столбце. Докажите, что найдутся две пары с одинаковой суммой.

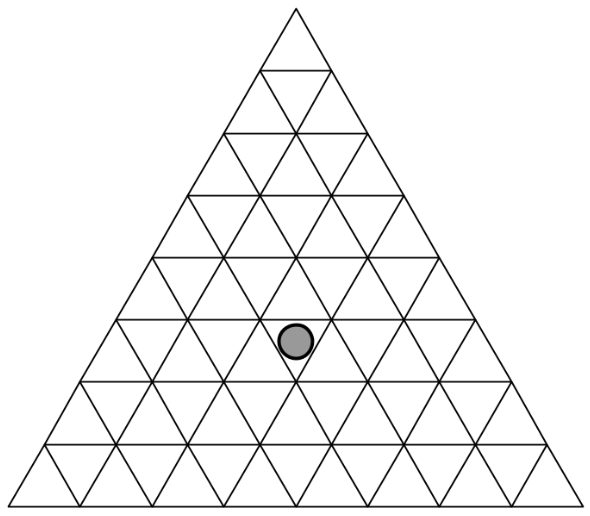
В центре треугольной доски стоит фишка (см. рисунок). Петя и Вася по очереди передвигают её в соседнее по стороне поле. Нельзя передвигать фишку в то поле, где она уже когда-то была (центральное поле считается посещённым). Проигрывает тот, кто не может сделать очередной ход. Кто может выиграть вне зависимости от игры соперника, если первым ходит Петя?