Открытая интернет-олимпиада по математике Меташколы, 4 класс, 2020 год, 1 этап
дата проведения: 21 октября 2020
Задача 6.
Сколько четырёхугольников можно найти на картинке?
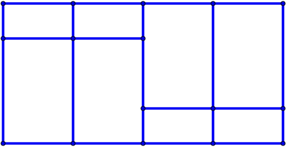
Ответ на Задачу 6.
Ответ: 22 четырёхугольника.
Решение:
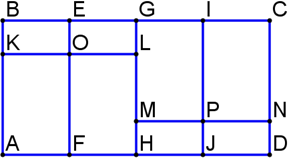
Считаем четырёхугольники по числу частей, из которых они состоят.
- Из 1 части состоит 8 четырёхугольников: AKOF, KBEO, FOLH, OEGL, HMPJ, MGIP, JPND, PICN
- Из 2 частей состоит 8 четырёхугольников: ABEF, FEGH, HGIJ, JICD, AKLH, KBGL, HMND, MGCN
- Из 3 частей не найдено
- Из 4 частей состоит 3 четырёхугольника: ABGH, FEIJ, HGCD
- Из 5 частей не найдено
- Из 6 частей состоит 2 четырёхугольника: ABIJ, FECD
- Из 7 частей не найдено
- Из 8 частей состоит большой четырёхугольник ABCD
Итого: 8 + 8 + 3 + 2 + 1 = 22 четырёхугольника.

