Открытая интернет-олимпиада по математике Меташколы, 6 класс, 2020 год, 1 этап
дата проведения: 23 октября 2020
источник: https://vivat2.okis.ru/metashkola
Задача 7.
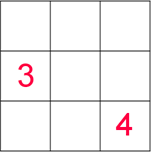
Запишите в свободные клетки квадрата числа, 5, 6, 7, 8, 9, 10, 11 так, чтобы суммы чисел во всех строках, столбцах и на двух диагоналях были бы равными. Какое число будет записано в верхней строке в угловой клетке справа?
Ответ на Задачу 7.
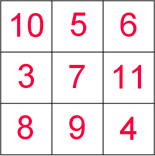
Ответ: В верхней строке в угловой клетке справа число 6.
Решение:
Сумма всех чисел: 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = 63.
Сумма чисел в каждой строке, в каждом столбце, на каждой диагонали: 63 : 3 = 21.
Все способы получения 21: 3+7+11, 3+8+10, 4+6+11, 4+7+10, 4+8+9, 5+6+10, 5+7+9, 6+7+8.
Число 7 входит в четыре тройки (строка, столбец, две диагонали), значит, в центральной клетке число 7.
